| << Chapter < Page | Chapter >> Page > |
KLASOPDRAG 1
Soos hoeke, kan driehoeke ook geklassifiseer word.
1. By die eerste klassifikasie kyk ons slegs na die hoeke van die driehoek.Kan jy die volgende voltooi?
a) Skerphoekige driehoeke is driehoeke met
b) Reghoekige driehoeke het
c) Stomphoekige driehoeke het
2. Klassifiseer die volgende driehoeke volgens hul hoeke (sonder die gebruik van ’n gradeboog)
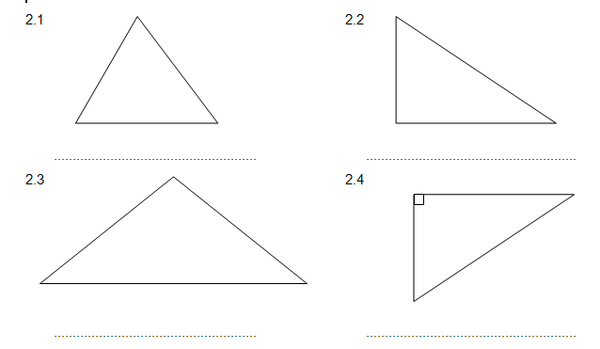
3. Die tweede klassifikasie is volgens die sye van die driehoek.Kan jy die volgende voltooi?
a) ’n Gelykbenige driehoek het
b) ’n Gelyksydige driehoek het
c) ’n Ongelyksydige driehoek se
4. Klassifiseer die volgende driehoeke volgens hul sye.
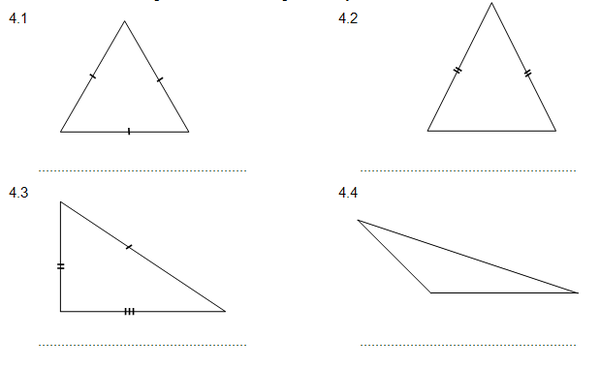
KLASOPDRAG 1
1. Om onbekende hoekgroottes sonder die gebruik van ’n gradeboog te bereken, is dit van kardinale belang om die volgende VIER STELLINGS deel van jou meetkunde kennis te maak.Kyk of jy die stellings kan voltooi en verduidelik die stelling dan aan die hand van jou eie voorbeeld (m.b.v. ’n skets)
1.1 Stelling 1:
Die som van die hoeke op ’n reguitlyn
Voorbeeld:
1.2 Stelling 2:
Regoorstaande of teenoorstaande hoeke is
Voorbeeld:
1.3 Stelling 3:
Die som van die binnehoeke van enige driehoek is
Voorbeeld: Om die stelling te bewys, moet jy die volgende instruksies uitvoer:
a) Teken enige driehoek op ’n stuk gekleurde papier en knip dit uit.
b) Merk die hoeke van die driehoek met die letters A, B en C.
c) Skeur die hoeke van die driehoek af.
d) Plak die hoeke van die driehoek langs mekaar op die lyn hier onder sodat die hoekpunte na die punt op die lyn wys.
Voltooi die volgende vergelyking: + + = ………°
(Let op die skryfwyse van die hoek.)
1.4 Stelling 4:
1.4.1 Alvorens ons na stelling 4 kan kyk, is dit belangrik dat die volgende terme vir jou baie duidelik is. Verklaar die volgende terme deur van ’n skets gebruik te maak:
1.4.2 Voltooi:
Die buitehoek van ’n driehoek is
Voorbeeld: (Maak gebruik van grade in jou skets.)
2. Bereken nou die groottes van die onbekende hoeke met redes.(Jou onderwyser sal jou help by die moeiliker voorbeelde.)
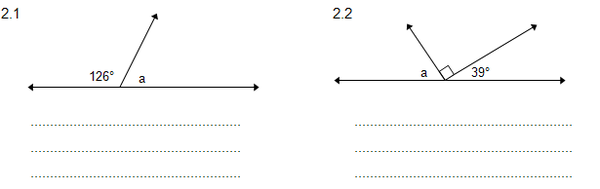
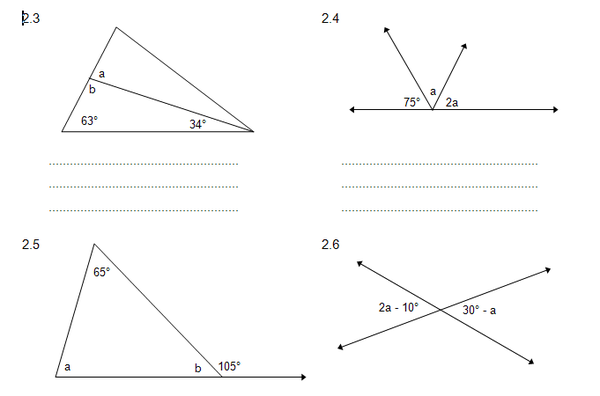
HUISWERKOPDRAG 1 EN 2
1. Voltooi elk van die volgende en gee redes vir die volgende stellings:
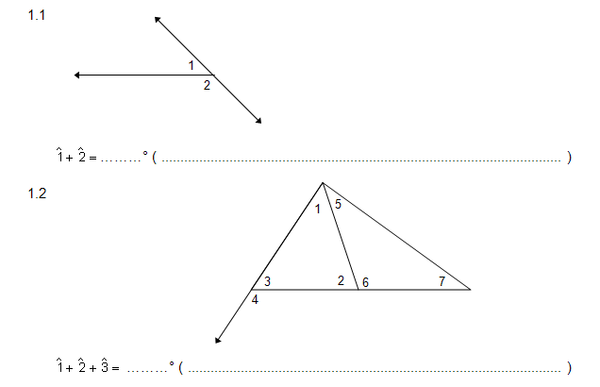
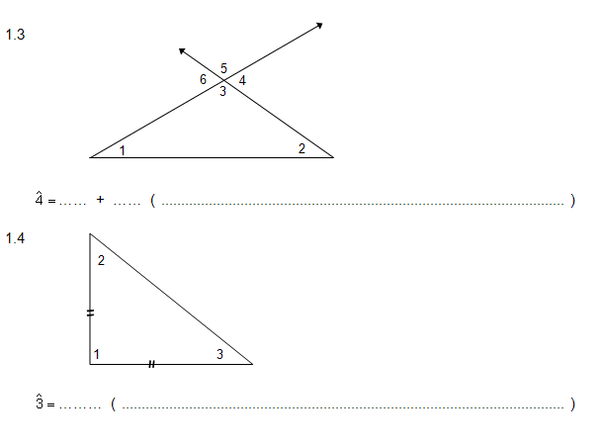
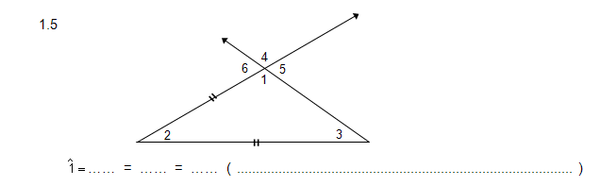
2. Bereken die groottes van elk van die onbekende hoeke en verstrek redes by elk.
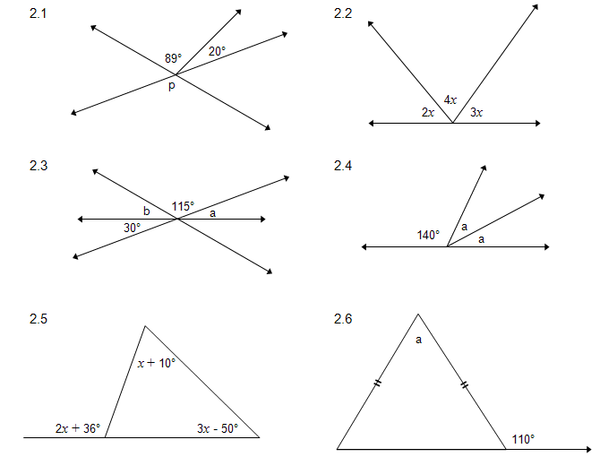
L e ereenhei d 3 Assessering 3.1
| Assessering van myself: | deur myself: | Assessering deur opvoeder: | |||||||||||||
| Ek kan… | | | | 1 | 2 | 3 | 4 | Kritieke Uitkomste | 1 | 2 | 3 | 4 | |||
| 1. enige grootte hoek konstrueer; (Lu 3.2 ; 4.7); | Kritiese en skeppende denke | ||||||||||||||
| 2. enige gegewe hoek klassifiseer; (Lu 3.2); | Deelname | ||||||||||||||
| 3. hoekgroottes m.b.v. ’n gradeboog bepaal; (Lu 3.2 ; 4.7); | Organisering en bestuur | ||||||||||||||
| 4. driehoeke klassifiseer volgens hulle hoeke en sye; (Lu 3.2 ; 3.3); | Prosessering van inligting | ||||||||||||||
| 5. stelling: som van hoeke op ’n reguitlyn toepas; (Lu 3.2); | Kommunikasie | ||||||||||||||
| 6. stelling: som van drie hoeke op ’n driehoek toepas; (Lu 3.2 ; 3.3); | Probleemoplossing | ||||||||||||||
| 7. stelling: die buitehoek van ’n driehoek = som van twee teenoordstaande binnehoeke toepas; (Lu 3.2 ; 3.3); | Selfstandigheid | ||||||||||||||
| 8. onbekende hoekgroottes bepaal deur 5 tot 7 toe te pas; (Lu 3.2; 3.3). |
goed gedeeltelik nie goed nie
| Kommentaar deur die leerder: | My plan van aksie: | My punte: | ||||||
| Ek is besonder tevrede met die standaard van my werk. | < | Datum : | ||||||
| Ek is tevrede met die vordering van my werk. | Uit: | |||||||
| Ek het hard gewerk, maar is nie tevrede met my prestasie nie. | Leerder : | |||||||
| Ek het nie my beste gelewer nie. | > |
| Kommentaar deur ouers: | Kommentaar deur opvoeder: | |
| Handtekening: Datum : | Handtekening: Datum : |
| LU 3 |
| Ruimte en Vorm (Meetkunde)Die leerder is in staat om eienskappe van en verwantskappe tussen twee- dimensionele vorms en drie-dimensionele voorwerpe in ’n verskeidenheid oriënta-sies en posisies te beskryf en voor te stel. |
| Dit word bewys as die leerder: |
| 3.2 in kontekste insluitend sodaniges wat gebruik word om sosiale-, kulturele- en omgewingsbewustheid aan te kweek, meetkundige figure in terme van kenmerke beskryf en klassifiseer, insluitend:3.2.1 sye, hoeke en diagonale (hoeklyne) en hulle verwantskappe, met die klem op driehoeke en vierhoeke (bv. soorte driehoeke en vierhoeke);3.3 woordeskat gebruik om parallelle te beskryf wat deur ‘n dwarslyn, loodlyne en snylyne gekruis word, asook driehoeke na aanleiding van hoekverwantskappe (bv. vertikaal teenoorstaande, ooreenkomstig). |
| LU 4 |
| MetingDie leerder is in staat om gepaste meeteenhede, -instrumente en formules in ’n verskeidenheid kontekste te gebruik. |
| Dit word bewys as die leerder: |
| 4.7 hoeke met behulp van ’n gradeboog akkuraat tot een graad kan skat, vergelyk, meet en teken. |
KLASWERKOPDRAG 1
Binnehoek
x = 130 0 – 50 0
= 80 0
= 54 0
2.2 180 0 – (90 0 + 39 0 ) (reguit lyn)
= 51 0
2.3 b = 180 0 – (63 0 + 34 0 ) (3 = 180 0 )
= 83 0
a = 180 0 – 83 (reguit lyn)
= 97 0 buitehoek = som van 2 teenoorstaande binnehoeke
2.4 3 a + 75 = 180 0 (reguit lyn)
3 a = 105 0
a = 35 0
= 75 0
a = 180 0 – (65 0 + 75 0 ) (3 = 180 0 )
= 40 0
3 a = 40
a =
a = 13,3 0
HUISWERKOPDRAG 1 EN 2
2.1 p = 89 0 + 20 0 (teenoorst. )
= 109 0
9 x = 180 0
x = 20 0
= 35 0
a = 180 0 – (115 0 + 35 0 ) (reguit lyn)
= 30 0
2 a = 40 0
a = 20 0
2.5 x + 10 0 + 3 x – 50 0 = 2 x + 36 0 (verlenging van )
x + 3 x – 2 x = 36 0 + 50 0 – 10 0
2 x = 76 0
x = 38 0
2.6 p = r = (180 0 – 110 0 ) (reguit lyn)
= 70 0 ( p = r , gelykbenige )
a = 180 0 – 140 0 ) (3 ∆ = 180 0 )
= 40 0

Notification Switch
Would you like to follow the 'Wiskunde graad 8' conversation and receive update notifications?