1. Home
  2. Wiskunde graad 8
  3. Kwartaal 2
  4. Hoeke wat ontstaan by ewewydige

2.4 Hoeke wat ontstaan by ewewydige (parallel) lyne

<< Chapter < Page
  Wiskunde graad 8   Page 1 / 1
Chapter >> Page >

Wiskunde

Graad 8

Heelgetalle, vergelykings en meetkunde

Module 11

Hoeke wat ontstaan by ewewydige (parallel) lyne

KLASOPDRAG 1

  • Kom ontdek stap vir stap meer omtrent ... Meetkunde .... tipes hoeke wat ontstaan by ewewydige (parallel) lyne en berekening van onbekende hoekgroottes deur die gebruik van jou vorige kennis.

1. Hoe sal jy weet wanneer twee lyne ewewydig is?

2. Hoe sal jy die volgende voorstelling in “wiskunde taal” voorstel?

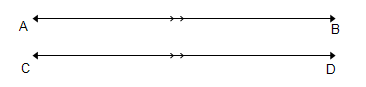
Jou antwoord:

3. Wat sal jy sê is ’n snylyn? Maak ’n skets om jou verduideliking te illustreer.

4. Watter drie tipes hoeke kan gevorm word, wanneer twee lyne ewewydig aanmekaar is?

5. Ja, verwisselende-, ooreenkomstige- en ko-binnehoeke kan slegs voorkom wanneer twee of meer lyne ewewydig aanmekaar is.

5.1 Kom ons kyk na: VERWISSELENDE HOEKE Dit kan so voorgestel word:

Jy kan ’n of vorm.

(Begin op die een ewewydige lyn en eindig weer op die ander ewewydige lyn.)

5.2 Kom ons kyk na: OOREENKOMSTIGE HOEKE Dit kan so voorgestel word:

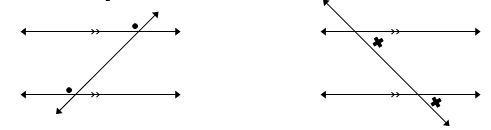
Jy kan ’n vorm.

(Altwee hoeke moet bokant of altwee aan die onderkant van die ewewydige lyne lê.)

5.3 Kom ons kyk na: KO-BINNEHOEKE Dit kan so voorgestel word:

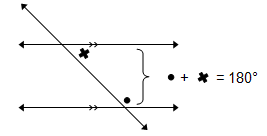
Die woord binnehoeke sê alles vir jou (altwee hoeke moet aan die binnekant van die twee ewewydige lyne lê. Belangrik: altwee hoeke moet ook aan dieselfde kant van die snylyn lê.

6. Gegee: Indien AB ll CD noem al die hoeke wat gelyk is a.g.v. die gegewe redes.

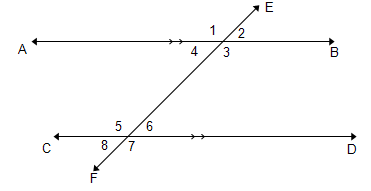
6.1 al die hoeke wat ooreenkomstige hoeke vorm (bv. 1 ˆ = 5 ˆ size 12{ { hat {1}}`=` { hat {5}}} {} ):

6.2 al die hoeke wat verwisselende hoeke vorm:

6.3 al die hoeke wat regoorstaande hoeke vorm:

6.4 al die hoeke wat ko-binnehoeke vorm:

7. Kyk nou of jy al die hoeke genommer van 1 tot 5 met redes kan bereken. (Sonder die gebruik van jou gradeboog.)Sodra jy ’n hoekgrootte bereken het, skryf dit op jou skets in.

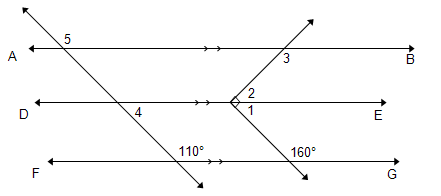
8. Bereken die volgende hoeke met redes:

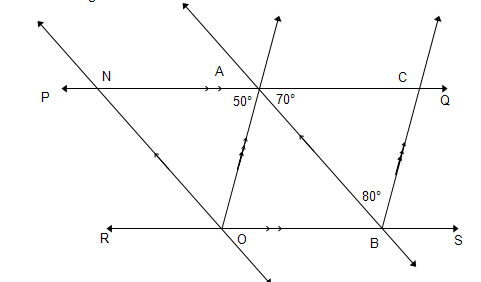
8.1 A O ˆ B size 12{A { hat {O}}B} {}

8.2 C B ˆ S size 12{C { hat {B}}S} {}

HUISWERKOPDRAG 1

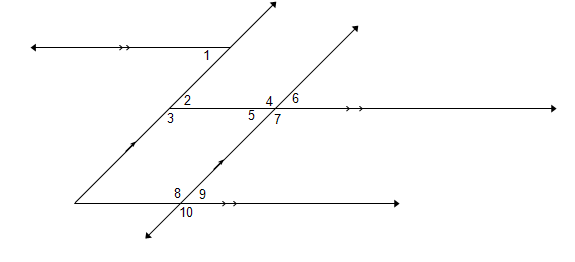
  1. Gee redes vir die volgende bewerings.

1.1 1 ˆ = 2 ˆ size 12{ { hat {1}}`=` { hat {2}}} {}

1.2 6 ˆ = 9 ˆ size 12{ { hat {6}}`=` { hat {9}}} {}

1.3 8 ˆ = 1 0 ˆ size 12{ { hat {8}}`=`1 { hat {0}}} {}

1.4 7 ˆ + 9 ˆ = 180 size 12{ { hat {7}}`+` { hat {9}}=`"180"} {} °

1.5 8 ˆ + 9 ˆ = 180 size 12{ { hat {8}}`+` { hat {9}}=`"180"} {} °

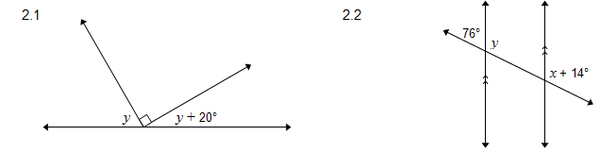
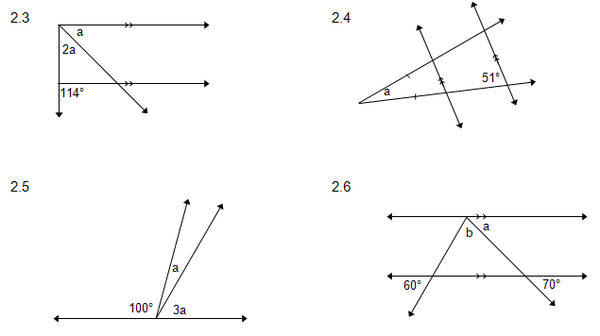
2. Bereken die onbekende hoeke in elk van die volgende met redes.

Assessering van myself: deur myself: Assessering deur opvoeder:
Ek kan… 1 2 3 4 Kritieke Uitkomste 1 2 3 4
1. verwisselende hoeke herken; (Lu 3.3); Kritiese en skeppende denke
2. ooreenkomstige hoeke herken; (Lu 3.3); Deelname
3. kan binnehoeke herken; (Lu 3.3); Organisering en bestuur
4. nr. 1 tot 3 gebruik om enige hoekgrootte te bereken; (Lu 3.3); Prosessering van inligting
5. sê wanneer twee lyne ewewydig is; (Lu 3.3); Kommunikasie
Probleemoplossing
Selfstandigheid

goed gedeeltelik nie goed nie

Kommentaar deur die leerder: My plan van aksie: My punte:
Ek is besonder tevrede met die standaard van my werk. < Datum :
Ek is tevrede met die vordering van my werk. Uit:
Ek het hard gewerk, maar is nie tevrede met my prestasie nie. Leerder :
Ek het nie my beste gelewer nie. >
Kommentaar deur ouers: Kommentaar deur opvoeder:
Handtekening: Datum : Handtekening: Datum :

Assessering

LU 3
Ruimte en Vorm (Meetkunde)Die leerder is in staat om eienskappe van en verwantskappe tussen twee- dimensionele vorms en drie-dimensionele voorwerpe in ’n verskeidenheid oriënta-sies en posisies te beskryf en voor te stel.
Dit word bewys as die leerder:
3.2 in kontekste insluitend sodaniges wat gebruik word om sosiale-, kulturele- en omgewingsbewustheid aan te kweek, meetkundige figure in terme van kenmerke beskryf en klassifiseer, insluitend:3.2.1 sye, hoeke en diagonale (hoeklyne) en hulle verwantskappe, met die klem op driehoeke en vierhoeke (bv. soorte driehoeke en vierhoeke);3.3 woordeskat gebruik om parallelle te beskryf wat deur ‘n dwarslyn, loodlyne en snylyne gekruis word, asook driehoeke na aanleiding van hoekverwantskappe (bv. vertikaal teenoorstaande, ooreenkomstig).

Memorandum

6.1 1 ˆ size 12{ {1} cSup { size 8{ widehat } } } {} = 5 ˆ size 12{ {5} cSup { size 8{ widehat } } } {} ; 2 ˆ size 12{ {2} cSup { size 8{ widehat } } } {} = 6 ˆ size 12{ {6} cSup { size 8{ widehat } } } {} ; 4 ˆ size 12{ {4} cSup { size 8{ widehat } } } {} = 8 ˆ size 12{ {8} cSup { size 8{ widehat } } } {} ; 3 ˆ size 12{ {3} cSup { size 8{ widehat } } } {} = 7 ˆ size 12{ {7} cSup { size 8{ widehat } } } {}

6.2 4 ˆ size 12{ {4} cSup { size 8{ widehat } } } {} = 6 ˆ size 12{ {6} cSup { size 8{ widehat } } } {} ; 3 ˆ size 12{ {3} cSup { size 8{ widehat } } } {} = 5 ˆ size 12{ {5} cSup { size 8{ widehat } } } {}

6.3 1 ˆ size 12{ {1} cSup { size 8{ widehat } } } {} = 3 ˆ size 12{ {3} cSup { size 8{ widehat } } } {} ; 4 ˆ size 12{ {4} cSup { size 8{ widehat } } } {} = 2 ˆ size 12{ {2} cSup { size 8{ widehat } } } {} ; 5 ˆ size 12{ {5} cSup { size 8{ widehat } } } {} = 7 ˆ size 12{ {7} cSup { size 8{ widehat } } } {} ; 8 ˆ size 12{ {8} cSup { size 8{ widehat } } } {} = 6 ˆ size 12{ {6} cSup { size 8{ widehat } } } {}

6.4 4 ˆ size 12{ {4} cSup { size 8{ widehat } } } {} + 5 ˆ size 12{ {5} cSup { size 8{ widehat } } } {} ; 3 ˆ size 12{ {3} cSup { size 8{ widehat } } } {} + 6 ˆ size 12{ {6} cSup { size 8{ widehat } } } {}

7. 1 ˆ size 12{ {1} cSup { size 8{ widehat } } } {} = 20 0 (ko-binnehoek; DE FG )

2 ˆ size 12{ {2} cSup { size 8{ widehat } } } {} = 70 0 (regte ∠ ) size 12{∠ \) } {}

3 ˆ size 12{ {3} cSup { size 8{ widehat } } } {} = 110 0 (ko-binnehoek; AB DE )

4 ˆ size 12{ {4} cSup { size 8{ widehat } } } {} = 70 0 (ko-binnehoek; DE FG )

5 ˆ size 12{ {5} cSup { size 8{ widehat } } } {} = 110 0 (ooreenkomstige ∠ e size 12{∠e} {} ; AB FG )

HUISWERKOPDRAG 1

  • Wissel
  • Ooreenkomstige (gelykstaande)
  • Vert. Teenoorstaande
  • Ko-binnehoek
  • Reguit lyn
  • y + 90 0 + y + 20 0 = 180 0 (Reguit lyn)

2 y = 70 0

y = 35 0

  • y = 104 0 (Reguit lyn)

x = 104 0 (ooreenkomstige ∠ e ) size 12{∠e \) } {}

x = 90 0

  • 3 a = 114 0 (ooreenkomstige ∠ e ) size 12{∠e \) } {}

a = 38 0

  • p = 51 0 (ooreenkomstige ∠ e ) size 12{∠e \) } {}

a = 180 0 – (51 0 + 51 0 ) (3 ∠ e size 12{∠e} {} ∆ = 180 0 )

a = 78 0

  • 3 a + a + 100 0 = 180 0 (Reguit lyn)

4 a + 100 0 = 180 0

40 a = 80 0

a = 20 0

  • a = 70 0

b = 180 0 – (60 0 + 70 0 ) (3 ∠ e size 12{∠e} {} ∆ = 180 0 )

b = 50 0

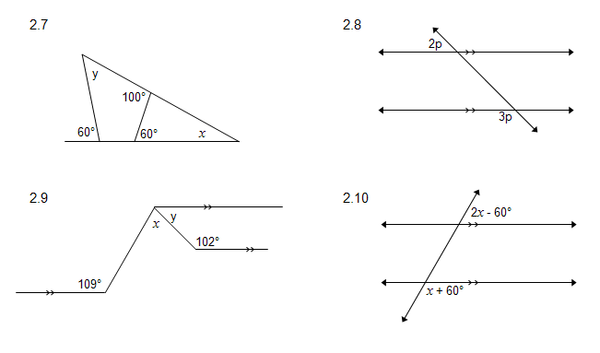
2.7 x = 180 0 – (80 0 + 60 0 ) (3 ∠ e size 12{∠e} {} ∆ = 180 0 )

x = 40 0

y = 360 0 – (120 0 + 120 0 + 100 0 )

= 20 0

2.8 2 p + 3 p = 180 0 (ko-binnehoek)

5 p = 180 0

p = 36 0

2.9 y = 78 0 (ko-binnehoek ∠ e ) size 12{∠e \) } {}

x + 78 0 = 109 0 (alt ∠ e ) size 12{∠e \) } {}

x = 31 0

2.10 2 x – 60 0 + x + 60 0 = 180 0 (ko-binnehoek)

3 x = 180 0

x = 60 0

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Wiskunde graad 8. OpenStax CNX. Sep 11, 2009 Download for free at http://cnx.org/content/col11033/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Wiskunde graad 8' conversation and receive update notifications?

Ask