| << Chapter < Page | Chapter >> Page > |
Let a square wave (period ) serve as the input to a first-order lowpass systemconstructed as a RC filter. We want to derive an expression for the time-domain response of the filter tothis input.
Simple circuits can implement simple mathematical operations, such as integration and differentiation. Wewant to develop an active circuit (it contains an op-amp) having an output that is proportional to theintegral of its input. For example, you could use an integrator in a car to determine distance traveled fromthe speedometer.
We determine where sound is coming from because we have two ears and a brain. Sound travels at a relativelyslow speed and our brain uses the fact that sound will arrive at one ear before the other. As shown here , a sound coming from the right arrives at the left ear seconds after it arrives at the right ear.
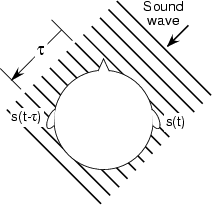
Once the brain finds this propagation delay, it can determine the sound direction. In an attempt to modelwhat the brain might do, RU signal processors want to design an optimal system that delays each ear's signal by some amount then adds themtogether. and are the delays applied to the left and right signalsrespectively. The idea is to determine the delay values according to some criterion that is based on what ismeasured by the two ears.
Architecting a system of modular components meansarranging them in various configurations to achieve some overall input-output relation. For each of the following , determine the overall transfer function between and .


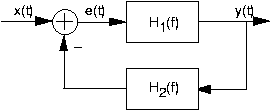
The overall transfer function for the cascade (first depicted system) is particularly interesting. What doesit say about the effect of the ordering of linear, time-invariant systems in a cascade?
Let the signal be the input to a linear, time-invariant filter having the transfer function shown below . Find the expression for , the filter's output.

Notification Switch
Would you like to follow the 'Fundamentals of electrical engineering i' conversation and receive update notifications?