| << Chapter < Page | Chapter >> Page > |
The parallelogram method is another graphical technique of finding the resultant of two vectors.
Method: The Parallelogram Method
A force of is applied to a block in a horizontal direction. A second force is applied to the object at an angle of above the horizontal.
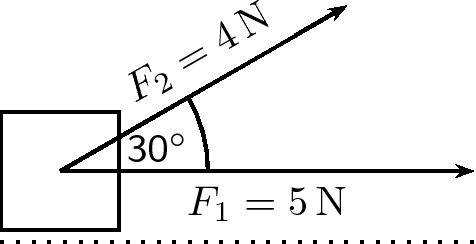
Determine the resultant force acting on the block using the parallelogram method of accurate construction.
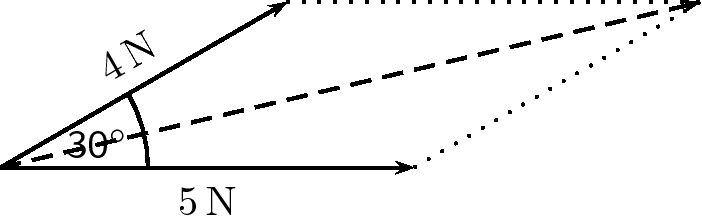
In this problem a scale of 1 cm = 1 N would be appropriate, since then the vector diagram would take up a reasonable fraction of the page. We can now begin the accurate scale diagram.
Let us draw first. According to the scale it has length 5 cm.
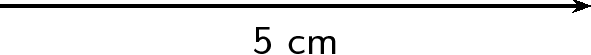
Next we draw . According to the scale it has length 4 cm. We make use of a protractor to draw this vector at to the horizontal.
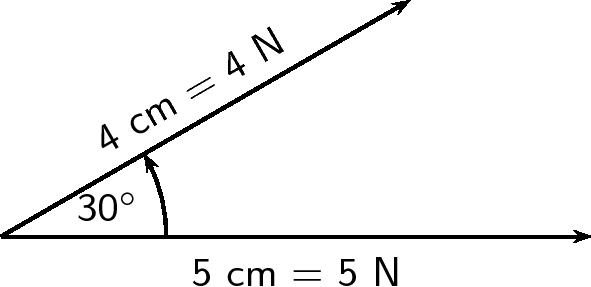
Next we complete the parallelogram and draw the diagonal.
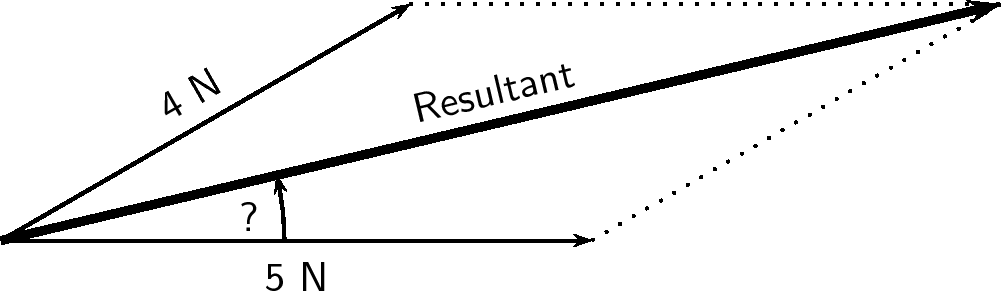
The resultant has a measured length of 8,7 cm.
We use a protractor to measure the angle between the horizontal and the resultant. We get .
Finally we use the scale to convert the measured length into the actual magnitude. Since 1 cm = 1 N, 8,7 cm represents 8,7 N. Therefore the resultant force is 8,7 N at above the horizontal.
The parallelogram method is restricted to the addition of just two vectors. However, it is arguably the most intuitive way of adding twoforces acting on a point.
Whenever you are faced with adding vectors acting in a straight line (i.e. some directed left and some right, or some acting up and others down) you can use a very simple algebraic technique:
Method: Addition/Subtraction of Vectors in a Straight Line
Let us consider a few examples.
A tennis ball is rolled towards a wall which is 10 m away from the ball. If after striking the wall the ball rolls a further 2,5 m along the ground away from the wall, calculate algebraically the ball's resultant displacement.
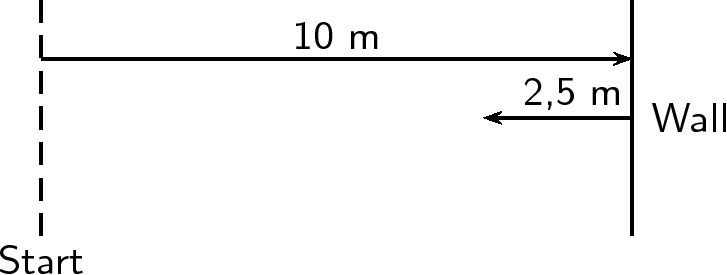
We know that the resultant displacement of the ball ( ) is equal to the sum of the ball's separate displacements ( and ):
Since the motion of the ball is in a straight line (i.e. the ball moves towards and away from the wall), we can use the method of algebraic additionjust explained.
Let's choose the positive direction to be towards the wall. This means that the negative direction is away from the wall.
With right positive:
Next we simply add the two displacements to give the resultant:
Finally, in this case towards the wall is the positive direction , so: = 7,5 m towards the wall.

Notification Switch
Would you like to follow the 'Physics - grade 10 [caps 2011]' conversation and receive update notifications?