Vectors (Page 9/10)

Physics - grade 10 [caps 2011]

Page 9 / 10

Block on an incline

As a further example of components let us consider a block of mass $m$ placed on a frictionless surface inclined at some angle $θ$ to the horizontal. The block will obviously slide down the incline, butwhat causes this motion?

The forces acting on the block are its weight $m g$ and the normal force $N$ exerted by the surface on the object. These two forces are shown in the diagram below.

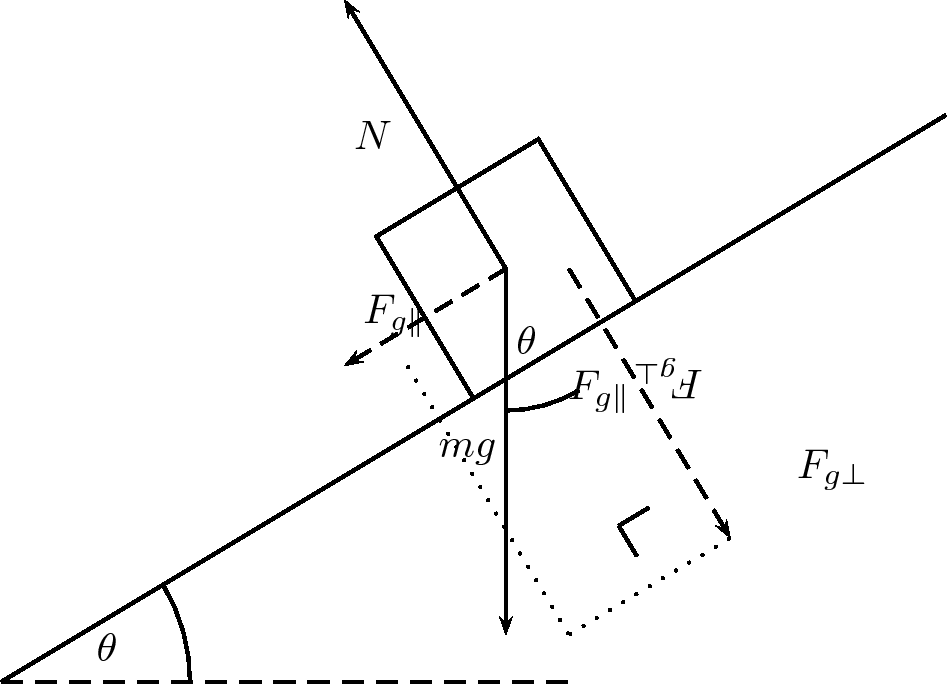
Now the object's weight can be resolved into components parallel and perpendicular to the inclined surface. These components are shown asdashed arrows in the diagram above and are at right angles to each other. The components have been drawn acting from the samepoint. Applying the parallelogram method, the two components of the block's weight sum to the weight vector.

To find the components in terms of the weight we can use trigonometry:

\begin{matrix} F_{g ∥} & = & m g sin θ \\ F_{g ⊥} & = & m g cos θ \end{matrix}

The component of the weight perpendicular to the slope $F_{g ⊥}$ exactly balances the normal force $N$ exerted by the surface. The parallel component, however, $F_{g ∥}$ is unbalanced and causes the block to slide down the slope.

Worked example

Determine the force needed to keep a 10 kg block from sliding down a frictionless slope. The slope makes an angle of $30^{\circ}$ with the horizontal.

Draw a diagram of the situation

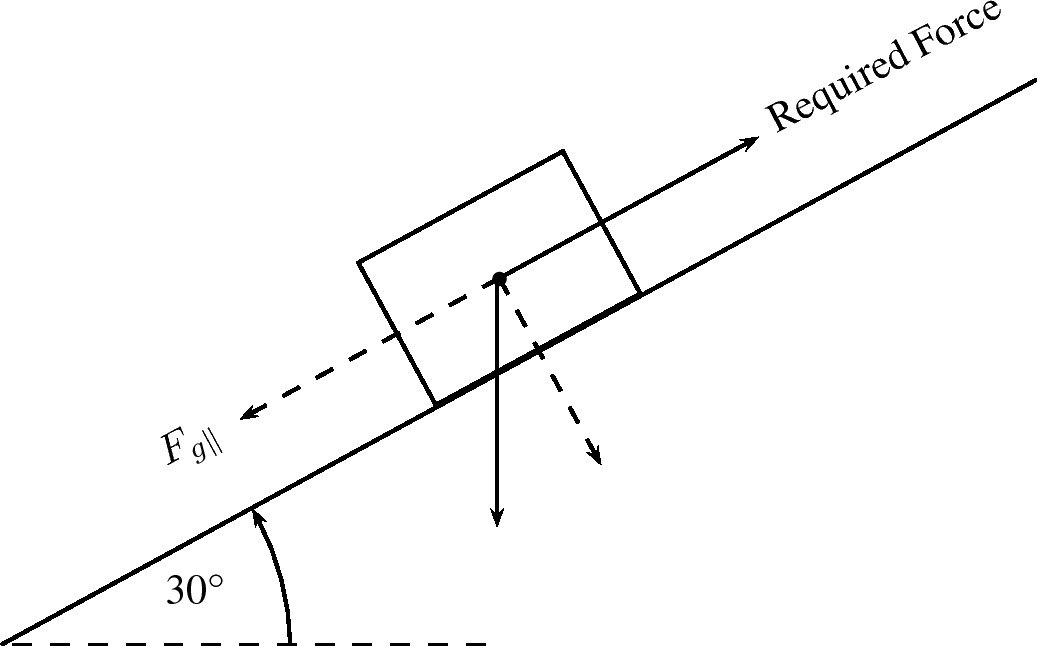
The force that will keep the block from sliding is equal to the parallel component of the weight, but its direction is up the slope.
Calculate $F_{g ∥}$
$\begin{matrix} F_{g ∥} & = & m g sin θ \\ = & (10) (9, 8) (sin 30^{\circ}) \\ = & 49 N \end{matrix}$
Write final answer
The force is 49 N up the slope.

Vector addition using components

Components can also be used to find the resultant of vectors. This technique can be applied to both graphical and algebraic methods of finding the resultant. The method is simple: make a rough sketch of the problem, find the horizontal and vertical components of each vector, find the sum of all horizontal components and the sum of all the vertical components and then use them to find the resultant.

Consider the two vectors, $\vec{A}$ and $\vec{B}$ , in [link] , together with their resultant, $\vec{R}$ .

An example of two vectors being added to give a resultant

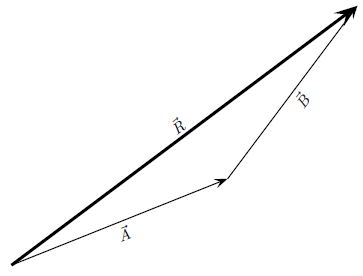
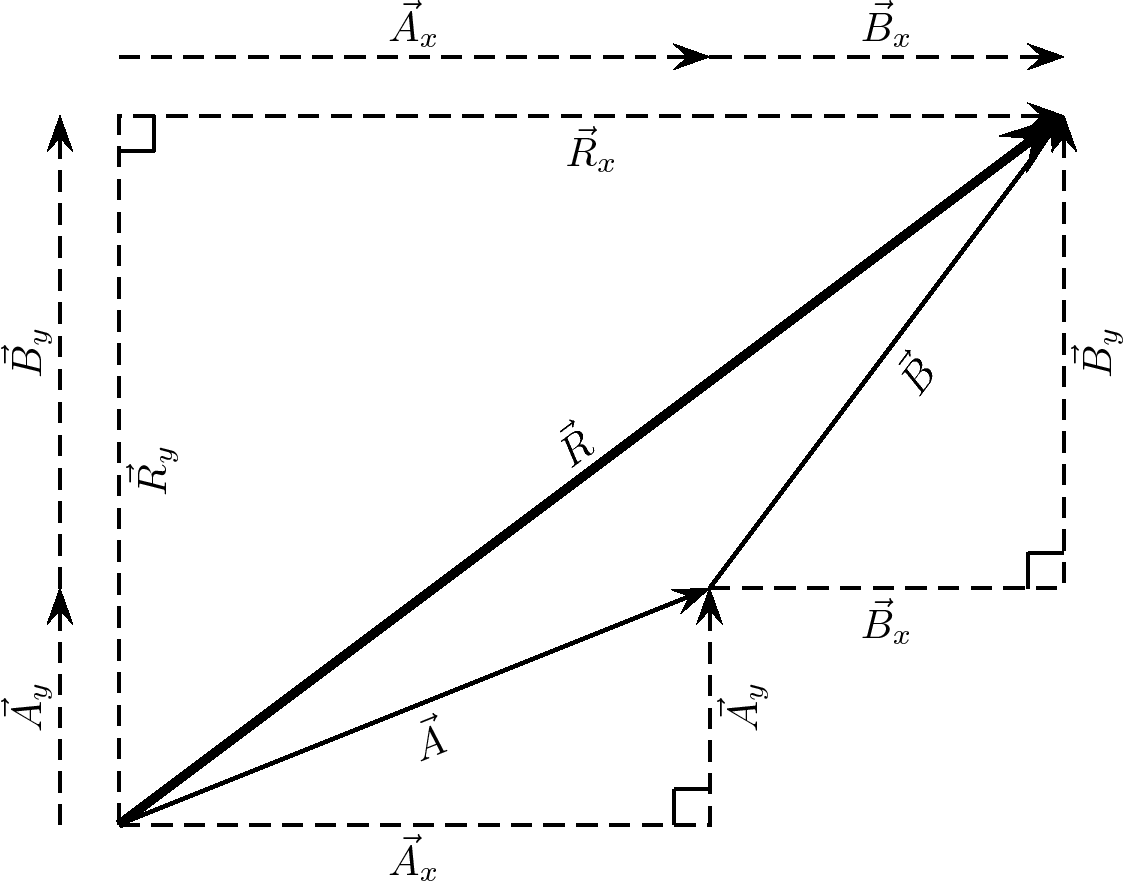
Each vector in [link] can be broken down into one component in the $x$ -direction (horizontal) and one in the $y$ -direction (vertical). These components are two vectors which when added give you the original vector as the resultant. This is shown in [link] where we can see that:

\begin{matrix} \vec{A} & = & {\vec{A}}_{x} + {\vec{A}}_{y} \\ \vec{B} & = & {\vec{B}}_{x} + {\vec{B}}_{y} \\ \vec{R} & = & {\vec{R}}_{x} + {\vec{R}}_{y} \end{matrix}

\begin{matrix} But, {\vec{R}}_{x} & = & {\vec{A}}_{x} + {\vec{B}}_{x} \\ and {\vec{R}}_{y} & = & {\vec{A}}_{y} + {\vec{B}}_{y} \end{matrix}

In summary, addition of the $x$ components of the two original vectors gives the $x$ component of the resultant. The same applies to the $y$ components. So if we just added all the components together we would get the same answer! This is another importantproperty of vectors.

If in [link] , $\vec{A} = 5, 385 m \cdot s^{- 1}$ at an angle of $21,8^{\circ}$ to the horizontal and $\vec{B} = 5 m \cdot s^{- 1}$ at an angle of $53,13^{\circ}$ to the horizontal, find $\vec{R}$ .

Decide how to tackle the problem
The first thing we must realise is that the order that we add the vectors does not matter. Therefore, we can work through the vectors to be added in any order.
Resolve $\vec{A}$ into components
We find the components of $\vec{A}$ by using known trigonometric ratios. First we find the magnitude of the vertical component, $A_{y}$ :

$\begin{matrix} sin θ & = & \frac{A_{y}}{A} \\ sin 21, 8^{\circ} & = & \frac{A_{y}}{5, 385} \\ A_{y} & = & (5, 385) (sin 21, 8^{\circ}) \\ = & 2 m \cdot s^{- 1} \end{matrix}$

Secondly we find the magnitude of the horizontal component, $A_{x}$ :

$\begin{matrix} cos θ & = & \frac{A_{x}}{A} \\ cos 21 . 8^{\circ} & = & \frac{A_{x}}{5, 385} \\ A_{x} & = & (5, 385) (cos 21, 8^{\circ}) \\ = & 5 m \cdot s^{- 1} \end{matrix}$

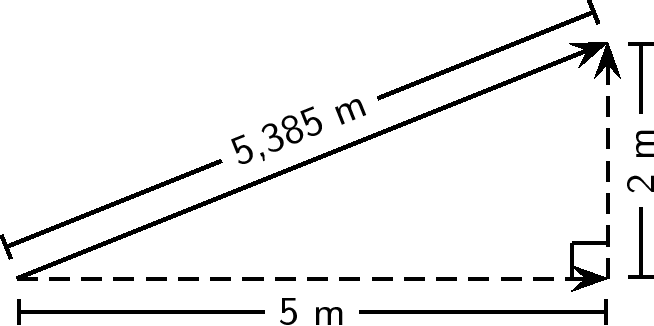
The components give the sides of the right angle triangle, for which the original vector, $\vec{A}$ , is the hypotenuse.
Resolve $\vec{B}$ into components
We find the components of $\vec{B}$ by using known trigonometric ratios. First we find the magnitude of the vertical component, $B_{y}$ :

$\begin{matrix} sin θ & = & \frac{B_{y}}{B} \\ sin 53, 13^{\circ} & = & \frac{B_{y}}{5} \\ B_{y} & = & (5) (sin 53, 13^{\circ}) \\ = & 4 m \cdot s^{- 1} \end{matrix}$

Secondly we find the magnitude of the horizontal component, $B_{x}$ :

$\begin{matrix} cos θ & = & \frac{B_{x}}{B} \\ cos 21, 8^{\circ} & = & \frac{B_{x}}{5, 385} \\ B_{x} & = & (5, 385) (cos 53, 13^{\circ}) \\ = & 5 m \cdot s^{- 1} \end{matrix}$
Determine the components of the resultant vector
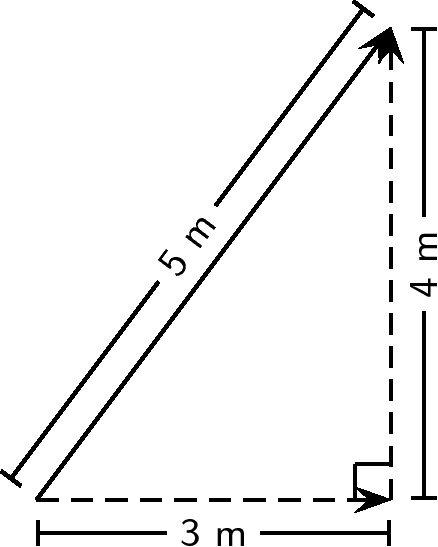
Now we have all the components. If we add all the horizontal components then we will have the $x$ -component of the resultant vector, ${\vec{R}}_{x}$ . Similarly, we add all the vertical components then we will have the $y$ -component of the resultant vector, ${\vec{R}}_{y}$ .

$\begin{matrix} R_{x} & = & A_{x} + B_{x} \\ = & 5 m \cdot s^{- 1} + 3 m \cdot s^{- 1} \\ = & 8 m \cdot s^{- 1} \end{matrix}$

Therefore, ${\vec{R}}_{x}$ is 8 m to the right.

$\begin{matrix} R_{y} & = & A_{y} + B_{y} \\ = & 2 m \cdot s^{- 1} + 4 m \cdot s^{- 1} \\ = & 6 m \cdot s^{- 1} \end{matrix}$

Therefore, ${\vec{R}}_{y}$ is 6 m up.
Determine the magnitude and direction of the resultant vector
Now that we have the components of the resultant, we can use the Theorem of Pythagoras to determine the magnitude of the resultant, $R$ .

$\begin{matrix} R^{2} & = & {(R_{x})}^{2} + {(R_{y})}^{2} \\ R^{2} & = & {(6)}^{2} + {(8)}^{2} \\ R^{2} & = & 100 \\ ∴ R & = & 10 m \cdot s^{- 1} \end{matrix}$

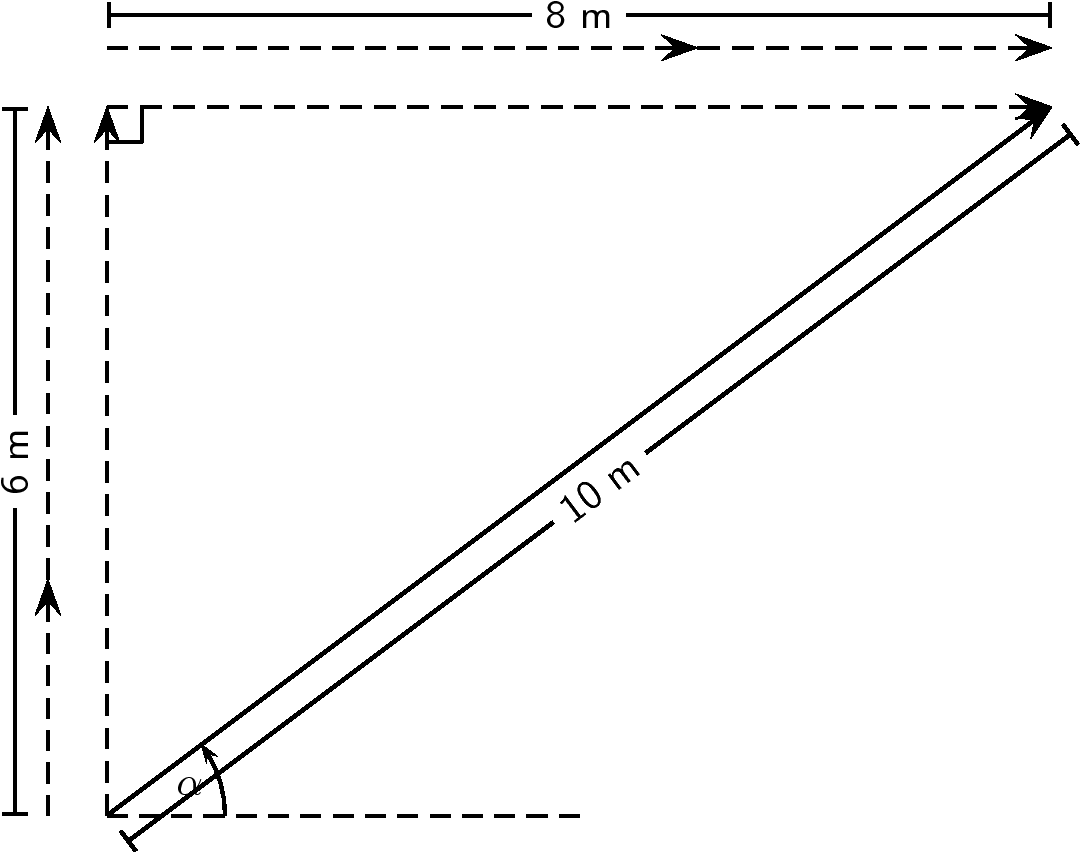
The magnitude of the resultant, $R$ is 10 m. So all we have to do is calculate its direction. We can specify the direction as the angle the vectors makes with a known direction. To do this you only need to visualise the vector as starting at the origin of a coordinate system. We have drawn this explicitly below and the angle we will calculate is labeled $α$ .

Using our known trigonometric ratios we can calculate the value of $α$ ;

$\begin{matrix} tan α & = & \frac{6 m \cdot s^{- 1}}{8 m \cdot s^{- 1}} \\ α & = & {tan}^{- 1} \frac{6 m \cdot s^{- 1}}{8 m \cdot s^{- 1}} \\ α & = & 36, 8^{\circ} \end{matrix}$
Quote the final answer
$\vec{R}$ is 10 m at an angle of $36, 8^{\circ}$ to the positive $x$ -axis.

Questions & Answers

I'm interested in biological psychology and cognitive psychology

Tanya Reply

what does preconceived mean

sammie Reply

physiological Psychology

Nwosu Reply

How can I develope my cognitive domain

Amanyire Reply

why is communication effective

Dakolo Reply

Communication is effective because it allows individuals to share ideas, thoughts, and information with others.

effective communication can lead to improved outcomes in various settings, including personal relationships, business environments, and educational settings. By communicating effectively, individuals can negotiate effectively, solve problems collaboratively, and work towards common goals.

it starts up serve and return practice/assessments.it helps find voice talking therapy also assessments through relaxed conversation.

miss

Every time someone flushes a toilet in the apartment building, the person begins to jumb back automatically after hearing the flush, before the water temperature changes. Identify the types of learning, if it is classical conditioning identify the NS, UCS, CS and CR. If it is operant conditioning, identify the type of consequence positive reinforcement, negative reinforcement or punishment

Wekolamo Reply

please i need answer

Wekolamo

because it helps many people around the world to understand how to interact with other people and understand them well, for example at work (job).

Manix Reply

Agreed 👍 There are many parts of our brains and behaviors, we really need to get to know. Blessings for everyone and happy Sunday!

ARC

A child is a member of community not society elucidate ?

JESSY Reply

Isn't practices worldwide, be it psychology, be it science. isn't much just a false belief of control over something the mind cannot truly comprehend?

Simon Reply

compare and contrast skinner's perspective on personality development on freud

namakula Reply

Skinner skipped the whole unconscious phenomenon and rather emphasized on classical conditioning

war

explain how nature and nurture affect the development and later the productivity of an individual.

Amesalu Reply

nature is an hereditary factor while nurture is an environmental factor which constitute an individual personality. so if an individual's parent has a deviant behavior and was also brought up in an deviant environment, observation of the behavior and the inborn trait we make the individual deviant.

Samuel

I am taking this course because I am hoping that I could somehow learn more about my chosen field of interest and due to the fact that being a PsyD really ignites my passion as an individual the more I hope to learn about developing and literally explore the complexity of my critical thinking skills

Zyryn Reply

good👍

Jonathan

and having a good philosophy of the world is like a sandwich and a peanut butter 👍

Jonathan

generally amnesi how long yrs memory loss

Kelu Reply

interpersonal relationships

Abdulfatai Reply

What would be the best educational aid(s) for gifted kids/savants?

Heidi Reply

treat them normal, if they want help then give them. that will make everyone happy

Saurabh

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Physics - grade 10 [caps 2011]. OpenStax CNX. Jun 14, 2011 Download for free at http://cnx.org/content/col11298/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Physics - grade 10 [caps 2011]' conversation and receive update notifications?

Ask

	2 Week 2 Social Psych By Yacoub Jayoghli Start Quiz
©flickr:	Math for Economists MCQ By Tony Pizur Start Quiz
©flickr: Alexander	Mechanics I MCQ By Stephanie Redfern Start Quiz
	1 SCJP/OCJP Java Certification By JavaChamp Team Start Exam
	Cultural Evolution Contemporary World By Richley Crapo Start Assignment
	Respiratory System Drugs By CB Biern Start Quiz
©flickr: Abraham	1 Biology 1 By Sarah Warren Start Test
	8 Sociology 08 Media and Technology MCQ By OpenStax Start Quiz
	30 Biology 30 Plant Form and Physiology MCQ By OpenStax Start Quiz
	31 Biology 31 Soil and Plant Nutrition MCQ By OpenStax Start Quiz