2.2 Evaluate, simplify, and translate expressions (Page 3/9)

Prealgebra Page 3 / 9

We can see why this works by writing both terms as addition problems.

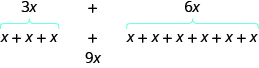
The image shows the expression 3 x plus 6 x. The 3 x represents x plus x plus x. The 6 x represents x plus x plus x plus x plus x plus x. The expression 3 x plus 6 x becomes x plus x plus x plus x plus x plus x plus x plus x plus x. This simplifies to a total of 9 x's or the term 9 x.

Add the coefficients and keep the same variable. It doesn’t matter what $x$ is. If you have $3$ of something and add $6$ more of the same thing, the result is $9$ of them. For example, $3$ oranges plus $6$ oranges is $9$ oranges. We will discuss the mathematical properties behind this later.

The expression $3 x + 6 x$ has only two terms. When an expression contains more terms, it may be helpful to rearrange the terms so that like terms are together. The Commutative Property of Addition says that we can change the order of addends without changing the sum. So we could rearrange the following expression before combining like terms.

The image shows the expression 3 x plus 4 y plus 2 x plus 6 y. The position of the middle terms, 4 y and 2 x, can be switched so that the expression becomes 3 x plus 2 x plus 4 y plus 6 y. Now the terms containing x are together and the terms containing y are together.

Now it is easier to see the like terms to be combined.

Combine like terms.

Identify like terms.
Rearrange the expression so like terms are together.
Add the coefficients of the like terms.

Simplify the expression: $3 x + 7 + 4 x + 5 .$

Solution


Identify the like terms.
Rearrange the expression, so the like terms are together.
Add the coefficients of the like terms.
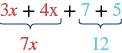The original expression is simplified to...

Got questions? Get instant answers now!

Simplify:

$7 x + 9 + 9 x + 8$

16 x + 17

Got questions? Get instant answers now!

Simplify:

$5 y + 2 + 8 y + 4 y + 5$

17 y + 7

Got questions? Get instant answers now!

Simplify the expression: $7 x^{2} + 8 x + x^{2} + 4 x .$

Solution


Identify the like terms.
Rearrange the expression so like terms are together.
Add the coefficients of the like terms.

These are not like terms and cannot be combined. So $8 x^{2} + 12 x$ is in simplest form.

Got questions? Get instant answers now!

Simplify:

$3 x^{2} + 9 x + x^{2} + 5 x$

4 x ² + 14 x

Got questions? Get instant answers now!

Simplify:

$11 y^{2} + 8 y + y^{2} + 7 y$

12 y ² + 15 y

Got questions? Get instant answers now!

Translate words to algebraic expressions

In the previous section, we listed many operation symbols that are used in algebra, and then we translated expressions and equations into word phrases and sentences. Now we’ll reverse the process and translate word phrases into algebraic expressions. The symbols and variables we’ve talked about will help us do that. They are summarized in [link]

Operation	Phrase	Expression
Addition	$a plus b$ $\begin{array}{l} the sum of a and b \end{array}$ $a increased by b$ $b more than a$ $\begin{array}{l} the total of a and b \end{array}$ $b added to a$	$a + b$
Subtraction	$a minus b$ $the difference of a and b$ $b subtracted from a$ $a decreased by b$ $b less than a$	$a - b$
Multiplication	$a times b$ $the product of a and b$	$a \cdot b, a b, a (b), (a) (b)$
Division	$a divided by b$ $the quotient of a and b$ $the ratio of a and b$ $b divided into a$	$a \div b, a / b, \frac{a}{b}, b a$

Operation	Phrase	Expression
Addition	$a$ plus $b$ the sum of $a$ and $b$ $a$ increased by $b$ $b$ more than $a$ the total of $a$ and $b$ $b$ added to $a$	$a + b$
Subtraction	$a$ minus $b$ the difference of $a$ and $b$ $b$ subtracted from $a$ $a$ decreased by $b$ $b$ less than $a$	$a - b$
Multiplication	$a$ times $b$ the product of $a$ and $b$	$a \cdot b$ , $a b$ , $a (b)$ , $(a) (b)$
Division	$a$ divided by $b$ the quotient of $a$ and $b$ the ratio of $a$ and $b$ $b$ divided into $a$	$a \div b$ , $a / b$ , $\frac{a}{b}$ , $b a$

Look closely at these phrases using the four operations:

the sum of $a$ and $b$
the difference of $a$ and $b$
the product of $a$ and $b$
the quotient of $a$ and $b$

Each phrase tells you to operate on two numbers. Look for the words of and and to find the numbers.

Translate each word phrase into an algebraic expression:

ⓐ the difference of $20$ and $4$
ⓑ the quotient of $10 x$ and $3$

Solution

ⓐ The key word is difference , which tells us the operation is subtraction. Look for the words of and and to find the numbers to subtract.

$\begin{array}{l} the difference of 20 a n d 4 \\ 20 minus 4 \\ 20 - 4 \end{array}$

ⓑ The key word is quotient , which tells us the operation is division.

$\begin{array}{l} the quotient of 10 x and 3 \\ divide 10 x by 3 \\ 10 x \div 3 \end{array}$

This can also be written as $\begin{array}{l} 10 x / 3 or \frac{10 x}{3} \end{array}$

Got questions? Get instant answers now!

Questions & Answers

what is microbiology

Agebe Reply

What is a cell

Odelana Reply

what is cell

Mohammed

how does Neisseria cause meningitis

Nyibol Reply

what is microbiologist

Muhammad Reply

what is errata

Muhammad

is the branch of biology that deals with the study of microorganisms.

Ntefuni Reply

What is microbiology

Mercy Reply

studies of microbes

Louisiaste

when we takee the specimen which lumbar,spin,

Ziyad Reply

How bacteria create energy to survive?

Muhamad Reply

Bacteria doesn't produce energy they are dependent upon their substrate in case of lack of nutrients they are able to make spores which helps them to sustain in harsh environments

_Adnan

But not all bacteria make spores, l mean Eukaryotic cells have Mitochondria which acts as powerhouse for them, since bacteria don't have it, what is the substitution for it?

Muhamad

they make spores

Louisiaste

what is sporadic nd endemic, epidemic

Aminu Reply

the significance of food webs for disease transmission

Abreham

food webs brings about an infection as an individual depends on number of diseased foods or carriers dully.

Mark

explain assimilatory nitrate reduction

Esinniobiwa Reply

Assimilatory nitrate reduction is a process that occurs in some microorganisms, such as bacteria and archaea, in which nitrate (NO3-) is reduced to nitrite (NO2-), and then further reduced to ammonia (NH3).

Elkana

This process is called assimilatory nitrate reduction because the nitrogen that is produced is incorporated in the cells of microorganisms where it can be used in the synthesis of amino acids and other nitrogen products

Elkana

Examples of thermophilic organisms

Shu Reply

Give Examples of thermophilic organisms

Shu

advantages of normal Flora to the host

Micheal Reply

Prevent foreign microbes to the host

Abubakar

they provide healthier benefits to their hosts

ayesha

They are friends to host only when Host immune system is strong and become enemies when the host immune system is weakened . very bad relationship!

Mark

what is cell

faisal Reply

cell is the smallest unit of life

Fauziya

cell is the smallest unit of life

Akanni

Innocent

cell is the structural and functional unit of life

Hasan

is the fundamental units of Life

Musa

what are emergency diseases

Micheal Reply

There are nothing like emergency disease but there are some common medical emergency which can occur simultaneously like Bleeding,heart attack,Breathing difficulties,severe pain heart stock.Hope you will get my point .Have a nice day ❣️

_Adnan

define infection ,prevention and control

Innocent

I think infection prevention and control is the avoidance of all things we do that gives out break of infections and promotion of health practices that promote life

Lubega

Heyy Lubega hussein where are u from?

_Adnan

en français

Adama

which site have a normal flora

ESTHER Reply

Many sites of the body have it Skin Nasal cavity Oral cavity Gastro intestinal tract

Safaa

skin

Asiina

skin,Oral,Nasal,GIt

Sadik

How can Commensal can Bacteria change into pathogen?

Sadik

How can Commensal Bacteria change into pathogen?

Sadik

all

Tesfaye

by fussion

Asiina

what are the advantages of normal Flora to the host

Micheal

what are the ways of control and prevention of nosocomial infection in the hospital

Micheal

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Prealgebra. OpenStax CNX. Jul 15, 2016 Download for free at http://legacy.cnx.org/content/col11756/1.9

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Prealgebra' conversation and receive update notifications?

Ask

	21 AP 21 Lymphatic Immune System Essay By OpenStax Start Flashcards
	11 Sociology 11 Race and Ethnicity MCQ By OpenStax Start Quiz
	1 CDL Quiz - Air Brakes Endorsement Part 1 By Jazzycazz Jackson Start Quiz
©flickr: Justin	The Last Holiday Concert Chapter 1 By Mackenzie Wilcox Start Quiz
	Algebra and trigonometry By OpenStax Read Online Course
©flickr: Gareth	Professional Etiquette MCQ By Abby Sharp Start Quiz
	25 AP 25 Urinary System MCQ By OpenStax Start Quiz
	Cultural Anthropology Assignment 2 By Richley Crapo Start Assignment
	American Government MCQ By Saylor Foundation Start Quiz
	9 BOD- Liver Quiz .... By Brooke Delaney Start Quiz