| << Chapter < Page | Chapter >> Page > |
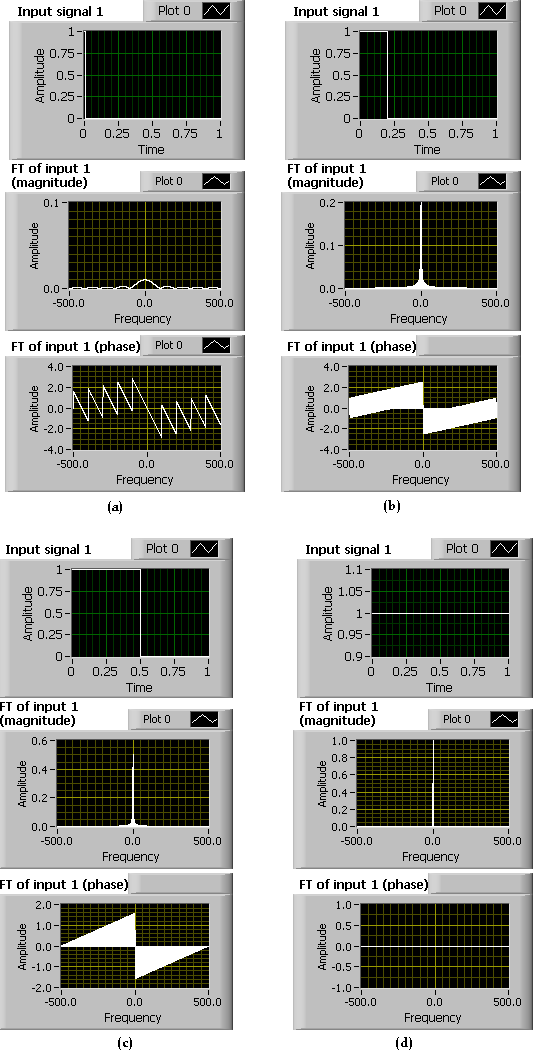
Keep the default values of Time shift (=0) and Time scaling (=1) and vary the Pulse width of the rectangular pulse. First, set the value of the Pulse width to its minimum value (=0.01) and then increase it. Observe that increasing the Pulse width in the time domain decrements the width in the frequency domain (see [link] ). When the Pulse width is set to its maximum value (=1) in the frequency domain, only one value can be seen at the center frequency indicating the signal is of DC type (refer to Properties of CTFT section of Chapter 5).
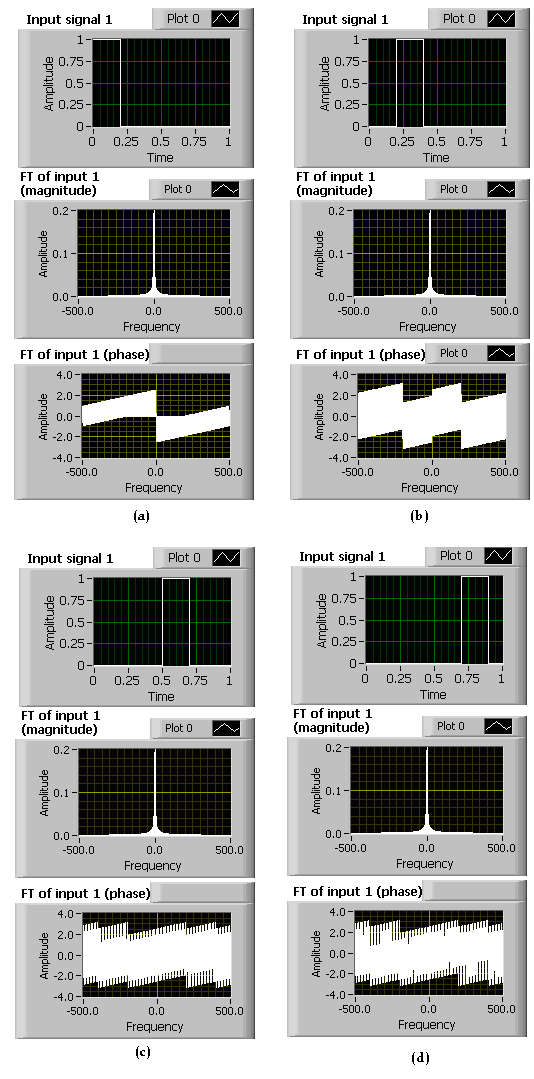
Next, for a fixed pulse width, vary the time shift. Observe that the phase spectrum changes but the magnitude spectrum remains the same. If the signal is shifted by a constant , its FT magnitude does not change, but the term gets added to its phase angle. This verifies the time-shifting property of FT as stated in Properties of CTFT section of Chapter 5 (see [link] ).
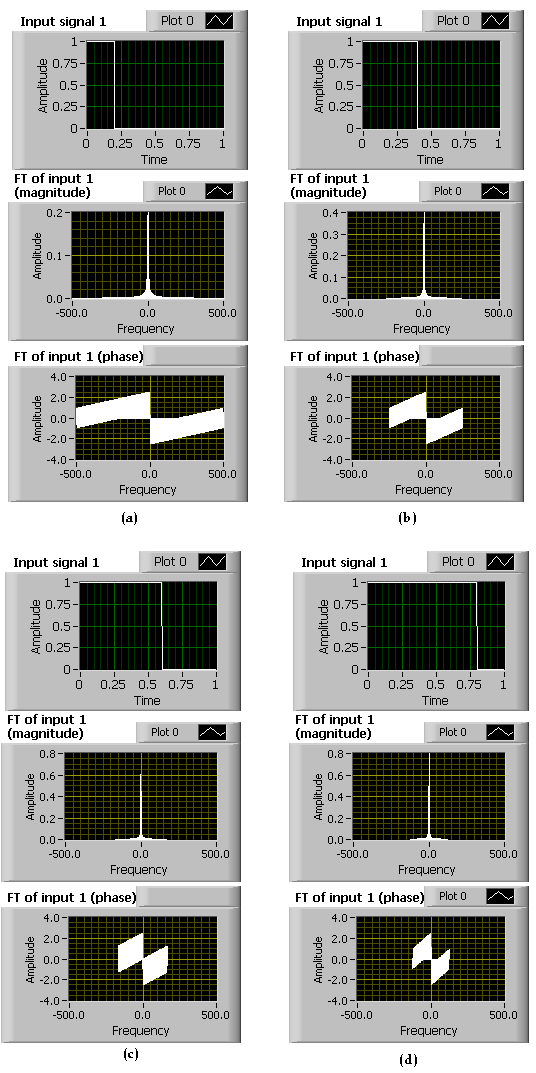
Observe that increasing the control Time scaling makes the spectrum wider. This indicates that compressing the signal in the time domain leads to expansion in the frequency domain. This verifies the time-scaling property of FT as stated in Properties of CTFT section of Chapter 5 (see [link] ).
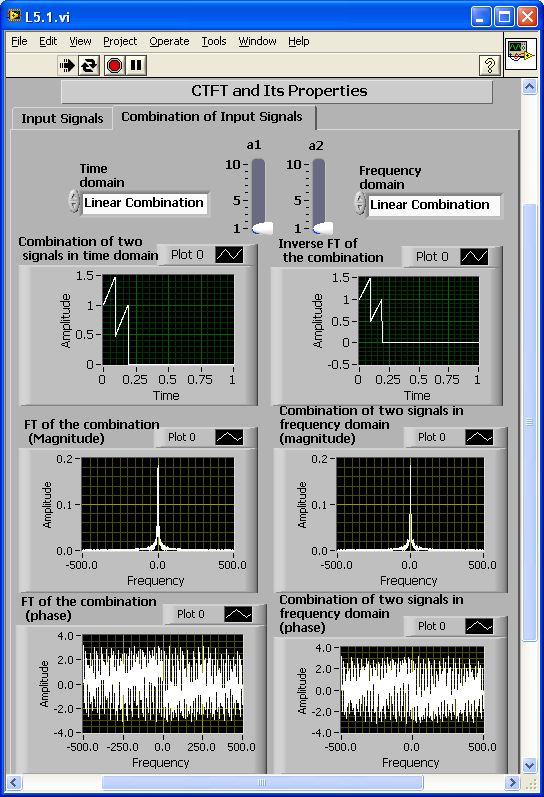
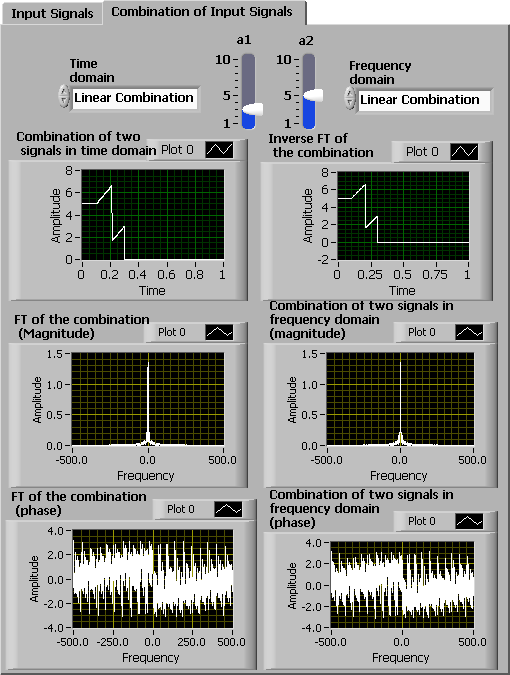
Here, combine two signals to examine the linearity property of FT. Select Linear Combination for the Time domain and Frequency domain combination method. This selection combines two time signals, and , linearly with the scaling factors, and , producing a new signal, . [link] displays the FT of this linear combination. The linear combination in the frequency domain produces a new signal, . [link] also displays the inverse FT of this combination. Observe that both combinations produce the same result in the time and frequency domains, as indicated by the linearity property stated in Properties of CTFT section of Chapter 5.
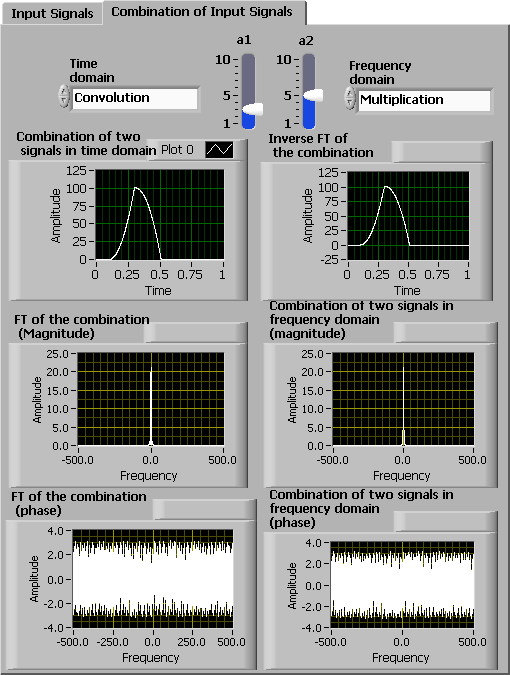
In this part, convolve two signals in the time domain to examine the time-convolution property of FT. Select Convolution for Time domain and Multiplication for Frequency domain. This selection produces and displays a new signal, , by convolving the two time signals and . Multiplication in the frequency domain produces a new signal, . The inverse FT of this multiplied signal is also displayed on the right. Note that both combinations produce the same outcome in the time and frequency domains. This verifies the time-convolution property stated in the Properties of CTFT section of Chapter 5 (see [link] ).
Convolve two signals in the frequency domain to examine the frequency-convolution property of FT. Select Convolution for Frequency domain and Multiplication for Time domain. This selection convolves the two time signals and to produce a new signal, . The inverse FT of the convolved signal is displayed. Multiplication in Time domain produces a new signal, . The FT of this multiplied signal is also displayed. Note that both combinations produce the same outcome in the time and frequency domains. This verifies the frequency-convolution property stated in the Properties of CTFT section of Chapter 5 (see [link] ).

Notification Switch
Would you like to follow the 'An interactive approach to signals and systems laboratory' conversation and receive update notifications?