| << Chapter < Page | Chapter >> Page > |
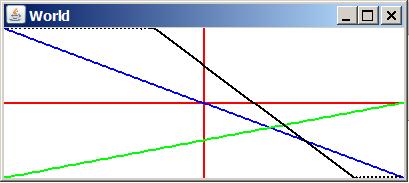
The code in Listing 3 initializes several variables and then calls a method named drawLine to implement the steps listed above to draw the BLUE line shown in Figure 3 .
double xScale = 1.0*world.getWidth()/2;
double yScale = 1.0*world.getHeight()/2;//Draw a line in BLUE.
turtle.setPenColor(Color.BLUE);double slope = 1.0;
double yIntercept = 0.0;drawLine(xScale,yScale,slope,yIntercept); Once again, I will put the run method on hold while we examine the code that actually draws the line as shown in Listing 4 .
void drawLine(double xScale,double yScale,
double slope,double yIntercept){double yVal = 0;
int row = 0;int col = 0;
double xVal = -1.0;for(int cnt=0; cnt<=100;cnt++,xVal += 0.02){
//Get a y-value for a given x-value.yVal = function(xVal,slope,yIntercept);//Scale the x and y values to match the plotting surface
col = (int)(xVal*xScale);row = (int)(yVal*yScale);
//Move to the first point without drawing a line because the// pen is not down. Translate the origin to the center in the
// process.turtle.moveTo(col + world.getWidth()/2,
row + world.getHeight()/2);//Lower the pen in order to draw a line from each point to the// next point.
turtle.penDown();}//end for loop
}//end drawLine method If you examine the code in Listing 4 along with values assigned to the variables in Listing 3 , you should be able to see the correlation between the code and the steps given earlier . In particular, you should be able to see how this code produces the BLUE lineshown in Figure 3 .
Note that the code in Listing 4 calls the method named function (shown in Listing 2 ) to get the values that define the line for the given slope and the given y-intercept value.
Returning to the run method, the code in Listing 5 repeats the process twice to draw the GREEN line and the BLACK line shown in Figure 3 for different slope and y-intercept values.
//Draw another line in GREEN.
turtle.penUp();turtle.setPenColor(Color.GREEN);
slope = -0.5;yIntercept = 0.5;
drawLine(xScale,yScale,slope,yIntercept);//Draw another line in BLACK.turtle.penUp();
turtle.setPenColor(Color.BLACK);slope = 2.0;
yIntercept = -0.5;drawLine(xScale,yScale,slope,yIntercept);
}//end run method Listing 5 also signals the end of the run method and the end of the program.
The program named Parabola01 shown in Listing 16 produces the graphic output shown in Figure 6 .
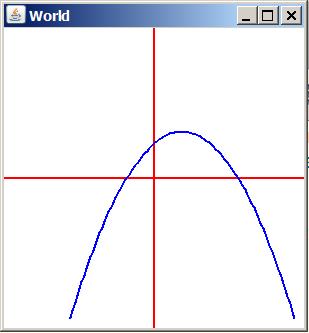
The method named function for the program named Parabola01 is shown in Listing 6 .
This method evaluates and returns the y-value for each incoming x-value for a parabola with no offsets centered at the origin as defined by the following equation:

Notification Switch
Would you like to follow the 'Object-oriented programming (oop) with java' conversation and receive update notifications?