Intervals and inversions

The distance between pitches

The interval between two notes is the distance between the two pitches - in other words, how much higher or lower one note is than the other. This concept is so important that it is almost impossible to talk about scales , chords , harmonic progression , cadence , or dissonance without referring to intervals. So if you want to learn music theory, it would be a good idea to spend some time getting comfortable with the concepts below and practicing identifying intervals.

Scientists usually describe the distance between two pitches in terms of the difference between their frequencies . Musicians find it more useful to talk about interval. Intervals can be described using half steps and whole steps . For example, you can say "B natural is a half step below C natural", or "E flat is a step and a half above C natural". But when we talk about larger intervals in the major/minor system , there is a more convenient and descriptive way to name them.

Naming intervals

The first step in naming the interval is to find the distance between the notes as they are written on the staff . Count every line and every space in between the notes, as well as the lines or spaces that the notes are on. This gives you the number for the interval.

Counting intervals

To find the interval, count the lines or spaces that the two notes are on as well as all the lines or spaces in between. The interval between B and D is a third. The interval between A and F is a sixth. Note that, at this stage, key signature , clef , and accidentals do not matter at all.

The simple intervals are one octave or smaller.

Simple intervals

If you like you can listen to each interval as written in [link] : prime , second , third , fourth , fifth , sixth , seventh , octave .

Compound intervals are larger than an octave.

Compound intervals

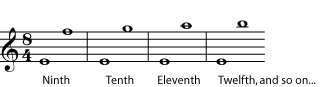
Listen to the compound intervals in [link] : ninth , tenth , eleventh .

Name the intervals.

Write a note that will give the named interval.

Classifying intervals

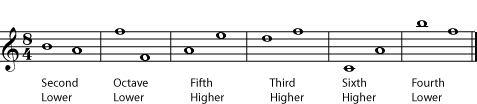
So far, the actual distance, in half-steps, between the two notes has not mattered. But a third made up of three half-steps sounds different from a third made up of four half-steps. And a fifth made up of seven half-steps sounds very different from one of only six half-steps. So in the second step of identifying an interval, clef , key signature , and accidentals become important.

Listen to the differences in the thirds and the fifths in [link] .

So the second step to naming an interval is to classify it based on the number of half steps in the interval. Familiarity with the chromatic scale is necessary to do this accurately.

Perfect intervals

Primes, octaves, fourths, and fifths can be perfect intervals.