| << Chapter < Page | Chapter >> Page > |
We now consider three simple but very important properties of addition.
Add the whole numbers
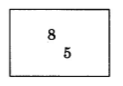
The numbers 8 and 5 can be added in any order. Regardless of the order they are added, the sum is 13.
Use the commutative property of addition to find the sum of 12 and 41 in two different ways.
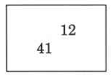
and
Use the associative property of addition to add the following whole numbers two different ways.
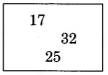
and
Add the whole numbers.

Zero added to 29 does not change the identity of 29.
Add the following whole numbers.
Suppose we let the letter x represent a choice for some whole number. For the first two problems, find the sums. For the third problem, find the sum provided we now know that x represents the whole number 17.
For the following problems, add the numbers in two ways.
For the following problems, show that the pairs of quantities yield the same sum.
The fact that (a first number + a second number) + third number = a first number + (a second number + a third number) is an example of the
The fact that 0 + any number = that particular number is an example of the
Identity
The fact that a first number + a second number = a second number + a first number is an example of the
Use the numbers 15 and 8 to illustrate the commutative property of addition.
Use the numbers 6, 5, and 11 to illustrate the associative property of addition.
The number zero is called the additive identity. Why is the term identity so appropriate?
…because its partner in addition remains identically the same after that addition
( [link] ) How many hundreds in 46,581?
( [link] ) Write 2,218 as you would read it.
Two thousand, two hundred eighteen.
( [link] ) Round 506,207 to the nearest thousand.
( [link] ) Find the difference:

Notification Switch
Would you like to follow the 'Fundamentals of mathematics' conversation and receive update notifications?