| << Chapter < Page | Chapter >> Page > |
In this section you will learn to:
If we consider the intersection of two lines in a plane, three things can happen.
The figures below shows all three cases.
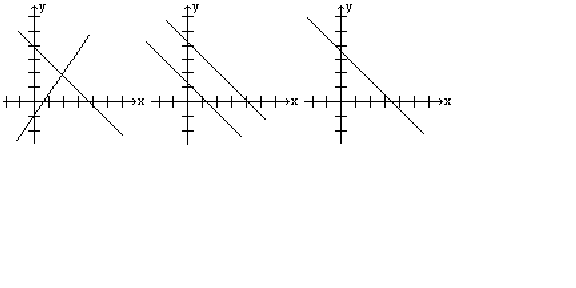
Every system of equations has either one solution, no solution, or infinitely many solutions.
In the [link] , we used the Gauss-Jordan method to solve systems that had exactly one solution. In this section, we will determine the systems that have no solution, and solve the systems that have infinitely many solutions.
Solve the following system of equations.
Let us use the Gauss-Jordan method to solve this system. The augmented matrix is as follows.
If we multiply the first row by – 1 and add to the second row, we get
Since 0 cannot equal 2, the last equation cannot be true for any choices of and .
Alternatively, it is clear that the two lines are parallel; therefore, they do not intersect.
At this stage, we are going to start using a calculator to row reduce the augmented matrix.
Solve the following system of equations.
We enter the following augmented matrix in the calculator.
Now by pressing the key to obtain the reduced row-echelon form, we get
The last row indicates that the system is inconsistent; therefore, there is no solution.
Solve the following system of equations.
The problem clearly asks for the intersection of two lines that are the same; that is, the lines coincide. This means the lines intersect at an infinite number of points.
A few intersection points are listed as follows: (3, 4), (5, 2), (–1, 8), (–6, 13) etc. However, when a system has an infinite number of solutions, the solution is often expressed in the parametric form. This can be accomplished by assigning an arbitrary constant, , to one of the variables, and then solving for the remaining variables. Therefore, if we let , then . Or we can say all ordered pairs of the form ( , ) satisfy the given system of equations.
Alternatively, while solving the Gauss-Jordan method, we will get the reduced row-echelon form given below.
The row of all zeros, can simply be discarded in a manner that it never existed. This leaves us with only one equation but two variables. And whenever there are more variables than the equations, the solution must be expressed in terms of an arbitrary constant, as above. That is, , .
Solve the following system of equations.
The augmented matrix and the reduced row-echelon form are given below.
Since the last equation dropped out, we are left with two equations and three variables. This means the system has infinite number of solutions. We express those solutions in the parametric form by letting the last variable equal the parameter .
The first equation reads , therefore, .
The second equation reads , therefore, .
And now if we let , the solution is expressed as follows:
The reader should note that particular solutions to the system can be obtained by assigning values to the parameter . For example, if we let , we have the solution (5, –5, 2).

Notification Switch
Would you like to follow the 'Applied finite mathematics' conversation and receive update notifications?