| << Chapter < Page | Chapter >> Page > |
represents the decay time constant for , which we set at 5 ms. represents the synaptic weight from the presynaptic cell i. holds all of the presynaptic spike times for a single cell. We use to denote the Dirac delta function (the unit impulse function). As such, cell conductance will decay exponentially without input and increase by the degree of the synaptic weight upon external stimulus or the firing of neighboring cells. Note that if there are multiple inputs, their effect on conductance is additive, resulting in faster cell depolarization.
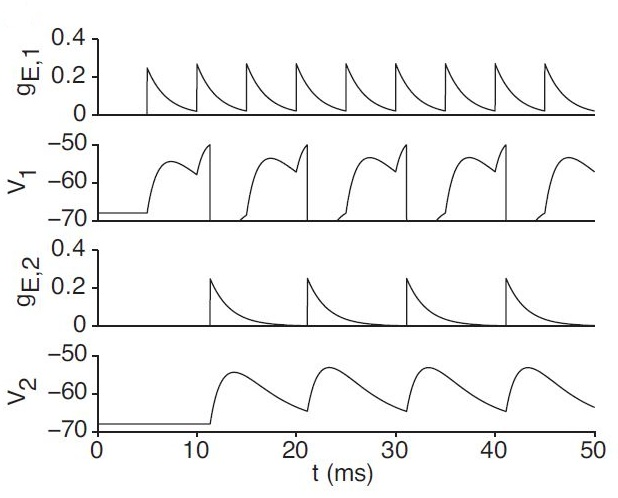
Having established the means by which we model our hippocampal place cells, we now turn to the question of how we modify our synaptic weights, which we answer in the next chapter.
| Parameter | Value | Description |
| -70 mV | Resting Membrane Potential | |
| -60 mV | Membrane Reset Potential | |
| -54 mV | Firing Threshold | |
| 5 ms | Refractory Period | |
| 1 mS/cm | Chloride (Leak) Conductance | |
| 20 F/cm | Membrane Capacitance | |
| 0 mV | Excitatory Synaptic Reversal Potential | |
| 5 ms | Synaptic Conductance Time Constant |
Synaptic plasticity is the ability of neurons to change the strength of their connections in response to certain stimuli or lack thereof. It is believed to play a major role in learning and the development of memories.
There exist several theories on how place cells in the hippocampus are involved in spatial memory. Most are based upon the fundamental concepts of synaptic plasticity: Hebbian learning and long term potentiation (LTP). They dictate that the synaptic weight, or the strength of the connection between two neurons, will increase (LTP) under certain conditions; such as an increased rate of firing or synchronized firing times; and decrease when the opposite occurs (which is known as long term depression, or LTD) [link] . The biological mechanisms of synaptic plasticity have not been fully elucidated, but it is believed to be dependent on the binding of glutamate receptors and signaling cascades dependent on calcium levels [link] .
In our discussion of synaptic plasticity, we aim to explain two distinct phenomena that we observe in Hippocampal Place Cells: (1): the backward shift in the firing of place fields (the region of the track in which the cell fires) and (2): the final stabilization of place fields. While there are other notable experimental phenomena in the experiments, such as expansion of place fields and increases in place cell firing rates, we will not discuss these in depth. We compare two different plasticity models: Spike-time Dependent Plasticity (STDP) and Calcium Dependent Plasticity (CaDP).
One of the most prominent plasticity theories is Spike Time-Dependent Plasticity (STDP), which dictates that an increase or decrease in synaptic weight between two cells is based upon the time between the firing of the cells and the order of the firing [link] . The magnitude of the synaptic weight change, ( ), is dictated by the following rule:

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?