Minterms  (Page 3/4)

The existence and uniqueness of the expansion is made plausible by simple examples utilizing minterm maps to determine graphically the minterm content of various Boolean combinations.Using the arrangement and numbering system introduced above, we let M _i represent the i th minterm (numbering from zero) and let $p\left(i\right)$ represent the probability of that minterm. When we deal with a union of minterms in a minterm expansion, it is convenient toutilize the shorthand illustrated in the following.

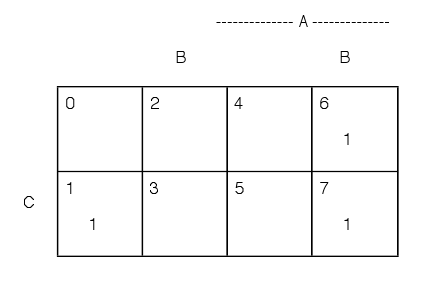
Consider the following simple example.

A key to establishing the expansion is to note that each minterm is either a subset of the combination or is disjoint from it. The expansion is thus the union of thoseminterms included in the combination. A general verification using indicator functions is sketched in the last section of this module.

Use of minterm maps

A typical problem seeks the probability of certain Boolean combinations of a class of events when the probabilities of various other combinations is given.We consider several simple examples and illustrate the use of minterm maps in formulation and solution.

Survey on software

Statistical data are taken for a certain student population with personal computers. An individual is selected at random. Let $A=$ the event the person selected has word processing, $B=$ the event he or she has a spread sheet program, and $C=$ the event the person has a data base program. The data imply

• The probability is 0.80 that the person has a word processing program: $P\left(A\right)=0.8$
• The probability is 0.65 that the person has a spread sheet program: $P\left(B\right)=0.65$
• The probability is 0.30 that the person has a data base program: $P\left(C\right)=0.3$
• The probability is 0.10 that the person has all three : $P\left(ABC\right)=0.1$
• The probability is 0.05 that the person has neither word processing nor spread sheet : $P\left(A^c{B}^c\right)=0.05$
• The probability is 0.65 that the person has at least two : $P(AB\cup AC\cup BC)=0.65$
• The probability of word processor and data base, but no spread sheet is twice the probabilty of spread sheet and data base, but no word processor : $P\left(A{B}^{c}C\right)=2P\left(A^{c}BC\right)$

1. What is the probability that the person has exactly two of the programs?
2. What is the probability that the person has only the data base program?

Several questions arise:

• Are these data consistent?
• Are the data sufficient to answer the questions?
• How may the data be utilized to anwer the questions?

SOLUTION

The data, expressed in terms of minterm probabilities, are:

$P\left(A\right)=p(4,5,6,7)=0.80$ ; hence $P\left(A^c\right)=p(0,1,2,3)=0.20$

$P\left(B\right)=p(2,3,6,7)=0.65$ ; hence $P\left(B^c\right)=p(0,1,4,5)=0.35$

$P\left(C\right)=p(1,3,5,7)=0.30$ ; hence $P\left(C^c\right)=p(0,2,4,6)=0.70$

$P\left(ABC\right)=p\left(7\right)=0.10P\left(A^c{B}^c\right)=p(0,1)=0.05$

$P(AB\cup AC\cup BC)=p(3,5,6,7)=0.65$