Right prisms and cylinders

Introduction

Geometry (Greek: geo = earth, metria = measure) arose as the field of knowledge dealing with spatial relationships. It was one of the two fields of pre-modern mathematics, the other being the study of numbers. In modern times, geometric concepts have become very complex and abstract and are barely recognizable as the descendants of early geometry.

Research project : history of geometry

Work in pairs or groups and investigate the history of the foundation of geometry. Describe the various stages of development and how the following cultures used geometry to improve their lives. This list should serve as a guideline and provide the minimum requirement, there are many other people who contributed to the foundation of geometry.

1. Ancient Indian geometry (c. 3000 - 500 B.C.)
   1. Harappan geometry
   2. Vedic geometry
2. Classical Greek geometry (c. 600 - 300 B.C.)
   1. Thales and Pythagoras
   2. Plato
3. Hellenistic geometry (c. 300 B.C - 500 C.E.)
   1. Euclid
   2. Archimedes

Right prisms and cylinders

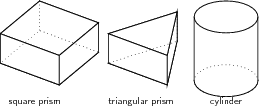
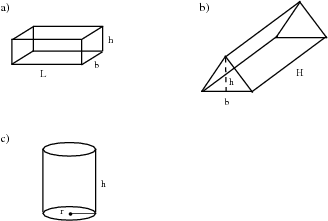
In this section we study how to calculate the surface areas and volumes of right prisms and cylinders. A right prism is a polygon that has been stretched out into a tube so that the height of the tube is perpendicular to the base. A square prism has a base that is a square and a triangular prism has a base that is a triangle.

It is relatively simple to calculate the surface areas and volumes of prisms.

Surface area

The term surface area refers to the total area of the exposed or outside surfaces of a prism. This is easier to understand if you imagine the prism as a solid object.

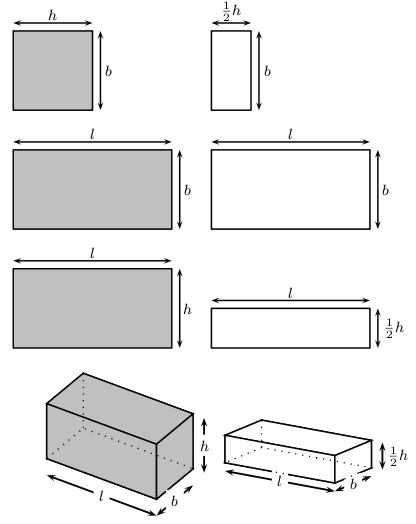
If you examine the prisms in [link] , you will see that each face of a prism is a simple polygon. For example, the triangular prism has two faces that are triangles and three faces that are rectangles. Therefore, in order to calculate the surface area of a prism you simply have to calculate the area of each face and add it up. In the case of a cylinder the top and bottom faces are circles, while the curved surface flattens into a rectangle.

Surface Area of Prisms

Calculate the area of each face and add the areas together to get the surface area. To do this you need to determine the correct shape of each and every face of the prism and then for each one determine the surface area. The sum of the surface areas of all the faces will give you the total surface area of the prism.

Discussion : surface areas

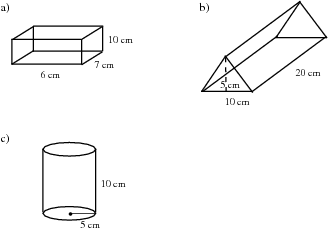
In pairs, study the following prisms and the adjacent image showing the various surfaces that make up the prism. Explain to your partner, how each relates to the other.

Surface areas

1. Calculate the surface area in each of the following:

   

2. If a litre of paint covers an area of $2m^2$ , how much paint does a painter need to cover:
   1. A rectangular swimming pool with dimensions $4m\times 3m\times 2,5m$ , inside walls and floor only.
   2. The inside walls and floor of a circular reservoir with diameter $4m$ and height $2,5m$

   

Volume

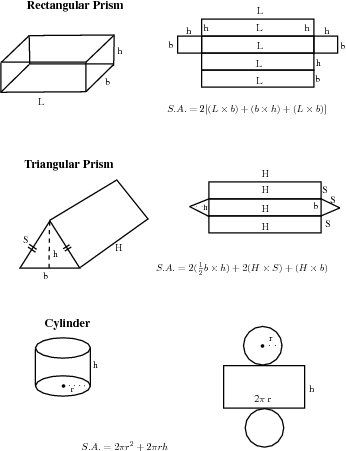
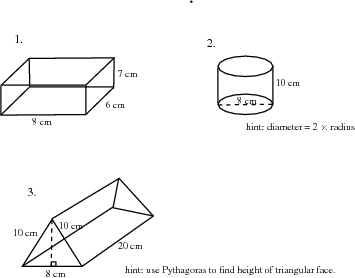
The volume of a right prism is calculated by multiplying the area of the base by the height. So, for a square prism of side length $a$ and height $h$ the volume is $a\times a\times h=a^{2}h$ .

Volume of Prisms

Calculate the area of the base and multiply by the height to get the volume of a prism.

Volume

1. Write down the formula for each of the following volumes:

   

2. Calculate the following volumes:

   

3. A cube is a special prism that has all edges equal. This means that each face is a square. An example of a cube is a die. Show that for a cube with side length $a$ , the surface area is $6a^2$ and the volume is $a^3$ .

   

Now, what happens to the surface area if one dimension is multiplied by a constant? For example, how does the surface area change when the height of a rectangular prism is divided by 2?

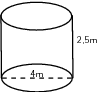
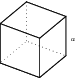
The size of a prism is specified by the length of its sides. The prism in the diagram has sides of lengths $L$ , $b$ and $h$ .

1. Consider enlarging all sides of the prism by a constant factor $x$ , where $x>1$ . Calculate the volume and surface area of the enlarged prism as a function of the factor $x$ and the volume of the original volume.
2. In the same way as above now consider the case, where $0<x<1$ . Now calculate the reduction factor in the volume and the surface area.

1. Identify

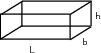
   The volume of a prism is given by: $V=L\times b\times h$

   The surface area of the prism is given by: $A=2\times (L\times b+L\times h+b\times h)$

2. Rescale

   If all the sides of the prism get rescaled, the new sides will be:

   $$\begin{array}{ccc}\hfill L^{\text{'}}& =& x\times L\hfill \\ \hfill b^{\text{'}}& =& x\times b\hfill \\ \hfill h^{\text{'}}& =& x\times h\hfill \end{array}$$

   The new volume will then be given by:

   $$\begin{array}{ccc}\hfill V^{\text{'}}& =& L^{\text{'}}\times b^{\text{'}}\times h^{\text{'}}\hfill \\ & =& x\times L\times x\times b\times x\times h\hfill \\ & =& x^3\times L\times b\times h\hfill \\ & =& x^3\times V\hfill \end{array}$$

   The new surface area of the prism will be given by:

   $$\begin{array}{ccc}\hfill A^{\text{'}}& =& 2\times (L^{\text{'}}\times b^{\text{'}}+L^{\text{'}}\times h^{\text{'}}+b^{\text{'}}\times h^{\text{'}})\hfill \\ & =& 2\times (x\times L\times x\times b+x\times L\times x\times h+x\times b\times x\times h)\hfill \\ & =& x^2\times 2\times (L\times b+L\times h+b\times h)\hfill \\ & =& x^2\times A\hfill \end{array}$$
3. Interpreting the above results
   1. We found above that the new volume is given by: $V^{\text{'}}=x^3\times V$ Since $x>1$ , the volume of the prism will be increased by a factor of $x^3$ . The surface area of the rescaled prism was given by: $A^{\text{'}}=x^2\times A$ Again, since $x>1$ , the surface area will be increased by a factor of $x^2$ . Surface areas which are two dimensional increase with the square of the factor while volumes, which are three dimensional, increase with the cube of the factor.
   2. The answer here is based on the same ideas as above. In analogy, since here $0<x<1$ , the volume will be reduced by a factor of $x^3$ and the surface area will be decreased by a factor of $x^2$

When the length of one of the sides is multiplied by a constant the effect is to multiply the original volume by that constant, as for the example in [link] .