| << Chapter < Page | Chapter >> Page > |
Our goal is to define a surface integral, and as a first step we have examined how to parameterize a surface. The second step is to define the surface area of a parametric surface. The notation needed to develop this definition is used throughout the rest of this chapter.
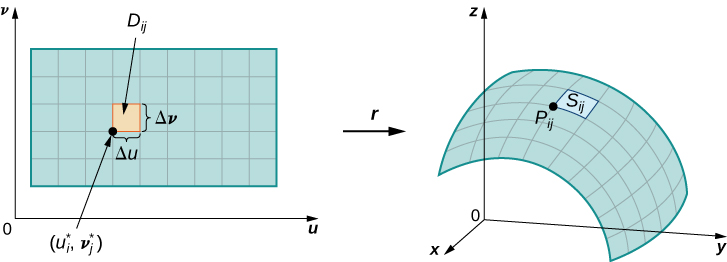
Let S be a surface with parameterization over some parameter domain D . We assume here and throughout that the surface parameterization is continuously differentiable—meaning, each component function has continuous partial derivatives. Assume for the sake of simplicity that D is a rectangle (although the following material can be extended to handle nonrectangular parameter domains). Divide rectangle D into subrectangles with horizontal width and vertical length Suppose that i ranges from 1 to m and j ranges from 1 to n so that D is subdivided into mn rectangles. This division of D into subrectangles gives a corresponding division of surface S into pieces Choose point in each piece Point corresponds to point in the parameter domain.
Note that we can form a grid with lines that are parallel to the u -axis and the v -axis in the uv -plane. These grid lines correspond to a set of grid curves on surface S that is parameterized by Without loss of generality, we assume that is located at the corner of two grid curves, as in [link] . If we think of r as a mapping from the uv -plane to the grid curves are the image of the grid lines under r . To be precise, consider the grid lines that go through point One line is given by the other is given by In the first grid line, the horizontal component is held constant, yielding a vertical line through In the second grid line, the vertical component is held constant, yielding a horizontal line through The corresponding grid curves are and and these curves intersect at point
Now consider the vectors that are tangent to these grid curves. For grid curve the tangent vector at is
For grid curve the tangent vector at is
If vector exists and is not zero, then the tangent plane at exists ( [link] ). If piece is small enough, then the tangent plane at point is a good approximation of piece
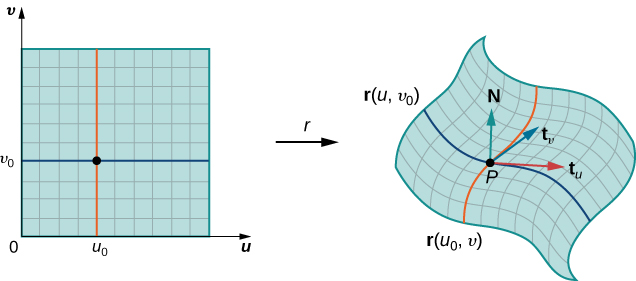
The tangent plane at contains vectors and and therefore the parallelogram spanned by and is in the tangent plane. Since the original rectangle in the uv -plane corresponding to has width and length the parallelogram that we use to approximate is the parallelogram spanned by and In other words, we scale the tangent vectors by the constants and to match the scale of the original division of rectangles in the parameter domain. Therefore, the area of the parallelogram used to approximate the area of is

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?