Polygons

Siyavula textbooks: grade 11 Page 1 / 1

Introduction

Extension : history of geometry

Work in pairs or groups and investigate the history of the development of geometry in the last 1500 years. Describe the various stages of development and how different cultures used geometry to improve their lives.

The works of the following people or cultures should be investigated:

Islamic geometry (c. 700 - 1500)
1. Thabit ibn Qurra
2. Omar Khayyam
3. Sharafeddin Tusi
Geometry in the 17th - 20th centuries (c. 700 - 1500)

Right pyramids, right cones and spheres

A pyramid is a geometric solid that has a polygon base and the base is joined to a point, called the apex. Two examples of pyramids are shown in the left-most and centre figures in [link] . The right-most figure has an apex which is joined to a circular base and this type of geometric solid is called a cone. Cones are similar to pyramids except that their bases are circles instead of polygons.

Examples of a square pyramid, a triangular pyramid and a cone.

Surface Area of a Pyramid

Khan academy video on solid geometry volumes

The surface area of a pyramid is calculated by adding the area of each face together.

If a cone has a height of $h$ and a base of radius $r$ , show that the surface area is $π r^{2} + π r \sqrt{r^{2} + h^{2}}$ .

Draw a picture
Identify the faces that make up the cone
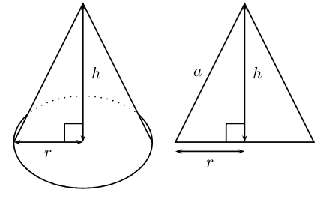
The cone has two faces: the base and the walls. The base is a circle of radius $r$ and the walls can be opened out to a sector of a circle.

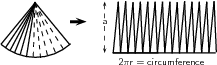
This curved surface can be cut into many thin triangles with height close to $a$ ( $a$ is called the slant height ). The area of these triangles will add up to $\frac{1}{2} \times$ base $\times$ height(of a small triangle) which is $\frac{1}{2} \times 2 π r \times a = π r a$
Calculate $a$
$a$ can be calculated by using the Theorem of Pythagoras. Therefore:

$a = \sqrt{r^{2} + h^{2}}$
Calculate the area of the circular base
$A_{b} = π r^{2}$
Calculate the area of the curved walls
$\begin{matrix} A_{w} & = & π r a \\ = & π r \sqrt{r^{2} + h^{2}} \end{matrix}$
Calculate surface area A
$\begin{matrix} A & = & A_{b} + A_{w} \\ = & π r^{2} + π r \sqrt{r^{2} + h^{2}} \end{matrix}$

Volume of a Pyramid: The volume of a pyramid is found by:

V = \frac{1}{3} A \cdot h

where $A$ is the area of the base and $h$ is the height.

A cone is like a pyramid, so the volume of a cone is given by:

V = \frac{1}{3} π r^{2} h .

A square pyramid has volume

V = \frac{1}{3} a^{2} h

where $a$ is the side length of the square base.

What is the volume of a square pyramid, 3cm high with a side length of 2cm?

Determine the correct formula
The volume of a pyramid is

$V = \frac{1}{3} A \cdot h$

where $A$ is the area of the base and $h$ is the height of the pyramid. For a square base this means

$V = \frac{1}{3} a \cdot a \cdot h$

where $a$ is the length of the side of the square base.
Substitute the given values
$\begin{matrix} = & \frac{1}{3} \cdot 2 \cdot 2 \cdot 3 \\ = & \frac{1}{3} \cdot 12 \\ = & 4 {cm}^{3} \end{matrix}$

We accept the following formulae for volume and surface area of a sphere (ball).

\begin{matrix} Surface area & = & 4 π r^{2} \\ Volume & = & \frac{4}{3} π r^{3} \end{matrix}

Surface area and volume

Calculate the volumes and surface areas of the following solids: *Hint for (e): find the perpendicular height using Pythagoras.
Water covers approximately 71% of the Earth's surface. Taking the radius of the Earth to be 6378 km, what is the total area of land (area not covered by water)?
A triangular pyramid is placed on top of a triangular prism. The prism has an equilateral triangle of side length 20 cm as a base, and has a height of 42 cm. The pyramid has a height of 12 cm.
1. Find the total volume of the object.
2. Find the area of each face of the pyramid.
3. Find the total surface area of the object.
Click here for the solution

Similarity of polygons

In order for two polygons to be similar the following must be true:

All corresponding angles must be congruent.
All corresponding sides must be in the same proportion to each other. Refer to the picture below: this means that the ratio of side $A E$ on the large polygon to the side $P T$ on the small polygon must be the same as the ratio of side $A B$ to side $P Q$ , $B C / Q R$ etc. for all the sides.

$\hat{A} = \hat{P}$ ; $\hat{B} = \hat{Q}$ ; $\hat{C} = \hat{R}$ ; $\hat{D} = \hat{S}$ ; $\hat{E} = \hat{T}$ and
$\frac{A B}{P Q} = \frac{B C}{Q R} = \frac{C D}{R S} = \frac{D E}{S T} = \frac{E A}{T P}$

then the polygons ABCDE and PQRST are similar.

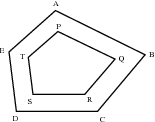
Polygons PQTU and PRSU are similar. Find the value of $x$ .

Identify corresponding sides
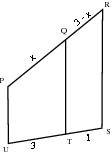
Since the polygons are similar,

$\begin{matrix} \frac{P Q}{P R} & = & \frac{T U}{S U} \\ ∴ \frac{x}{x + (3 - x)} & = & \frac{3}{4} \\ ∴ \frac{x}{3} & = & \frac{3}{4} \\ ∴ x & = & \frac{9}{4} \end{matrix}$

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Siyavula textbooks: grade 11 maths. OpenStax CNX. Aug 03, 2011 Download for free at http://cnx.org/content/col11243/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Siyavula textbooks: grade 11 maths' conversation and receive update notifications?

Ask

	Microeconomics Test 1 By IES Portal Start Test
	45 Biology 45 Population and Community Ecology MCQ By OpenStax Start Quiz
	Clinical Issues in TB Management By Cath Yu Start Quiz
	10 Clin Sci I - GI Twedt quiz By Brooke Delaney Start Quiz
	2 SCEA Java Architect By JavaChamp Team Start Exam
	17 Biology 17 Biotechnology and Genomics MCQ By OpenStax Start Quiz
©flickr:	Word Roots and Prefixes By Ellie Banfield Start Quiz
	10 Psychology MCQ 2011 Final Exam By John Gabrieli Start Exam
	16 AP 16 Neurological Essay Exam By OpenStax Start Flashcards
	Macroeconomics By OpenStax Read Online Course