| << Chapter < Page | Chapter >> Page > |
People could be sent very large distances (thousands or even millions of light years) and age only a few years on the way if they traveled at extremely high velocities. But, like emigrants of centuries past, they would leave the Earth they know forever. Even if they returned, thousands to millions of years would have passed on the Earth, obliterating most of what now exists. There is also a more serious practical obstacle to traveling at such velocities; immensely greater energies than classical physics predicts would be needed to achieve such high velocities. This will be discussed in Relatavistic Energy .
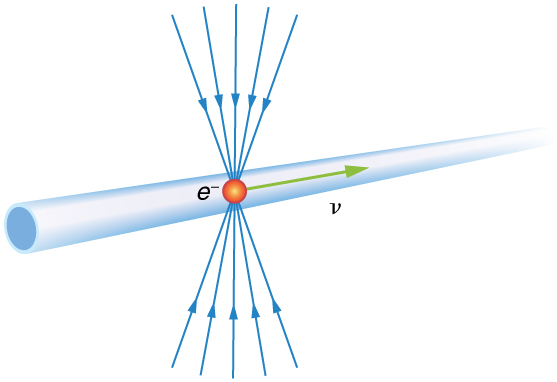
Why don’t we notice length contraction in everyday life? The distance to the grocery shop does not seem to depend on whether we are moving or not. Examining the equation , we see that at low velocities ( ) the lengths are nearly equal, the classical expectation. But length contraction is real, if not commonly experienced. For example, a charged particle, like an electron, traveling at relativistic velocity has electric field lines that are compressed along the direction of motion as seen by a stationary observer. (See [link] .) As the electron passes a detector, such as a coil of wire, its field interacts much more briefly, an effect observed at particle accelerators such as the 3 km long Stanford Linear Accelerator (SLAC). In fact, to an electron traveling down the beam pipe at SLAC, the accelerator and the Earth are all moving by and are length contracted. The relativistic effect is so great than the accelerator is only 0.5 m long to the electron. It is actually easier to get the electron beam down the pipe, since the beam does not have to be as precisely aimed to get down a short pipe as it would down one 3 km long. This, again, is an experimental verification of the Special Theory of Relativity.
A particle is traveling through the Earth’s atmosphere at a speed of . To an Earth-bound observer, the distance it travels is 2.50 km. How far does the particle travel in the particle’s frame of reference?
To whom does an object seem greater in length, an observer moving with the object or an observer moving relative to the object? Which observer measures the object’s proper length?
Relativistic effects such as time dilation and length contraction are present for cars and airplanes. Why do these effects seem strange to us?
Suppose an astronaut is moving relative to the Earth at a significant fraction of the speed of light. (a) Does he observe the rate of his clocks to have slowed? (b) What change in the rate of Earth-bound clocks does he see? (c) Does his ship seem to him to shorten? (d) What about the distance between stars that lie on lines parallel to his motion? (e) Do he and an Earth-bound observer agree on his velocity relative to the Earth?
A spaceship, 200 m long as seen on board, moves by the Earth at . What is its length as measured by an Earth-bound observer?
48.6 m
How fast would a 6.0 m-long sports car have to be going past you in order for it to appear only 5.5 m long?
(a) How far does the muon in [link] travel according to the Earth-bound observer? (b) How far does it travel as viewed by an observer moving with it? Base your calculation on its velocity relative to the Earth and the time it lives (proper time). (c) Verify that these two distances are related through length contraction .
(a) 1.387 km = 1.39 km
(b) 0.433 km
(c)
Thus, the distances in parts (a) and (b) are related when .
(a) How long would the muon in [link] have lived as observed on the Earth if its velocity was ? (b) How far would it have traveled as observed on the Earth? (c) What distance is this in the muon’s frame?
(a) How long does it take the astronaut in [link] to travel 4.30 ly at (as measured by the Earth-bound observer)? (b) How long does it take according to the astronaut? (c) Verify that these two times are related through time dilation with as given.
(a) 4.303 y (to four digits to show any effect)
(b) 0.1434 y
(c)
Thus, the two times are related when .
(a) How fast would an athlete need to be running for a 100-m race to look 100 yd long? (b) Is the answer consistent with the fact that relativistic effects are difficult to observe in ordinary circumstances? Explain.
Unreasonable Results
(a) Find the value of for the following situation. An astronaut measures the length of her spaceship to be 25.0 m, while an Earth-bound observer measures it to be 100 m. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
(a) 0.250
(b) must be ≥1
(c) The Earth-bound observer must measure a shorter length, so it is unreasonable to assume a longer length.
Unreasonable Results
A spaceship is heading directly toward the Earth at a velocity of . The astronaut on board claims that he can send a canister toward the Earth at relative to the Earth. (a) Calculate the velocity the canister must have relative to the spaceship. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?