| << Chapter < Page | Chapter >> Page > |
Convert point from Cartesian coordinates to cylindrical coordinates.
The use of cylindrical coordinates is common in fields such as physics. Physicists studying electrical charges and the capacitors used to store these charges have discovered that these systems sometimes have a cylindrical symmetry. These systems have complicated modeling equations in the Cartesian coordinate system, which make them difficult to describe and analyze. The equations can often be expressed in more simple terms using cylindrical coordinates. For example, the cylinder described by equation in the Cartesian system can be represented by cylindrical equation
Describe the surfaces with the given cylindrical equations.
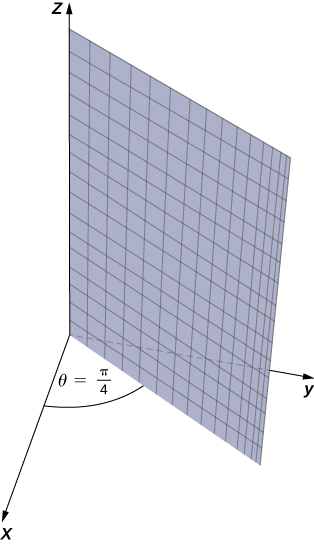
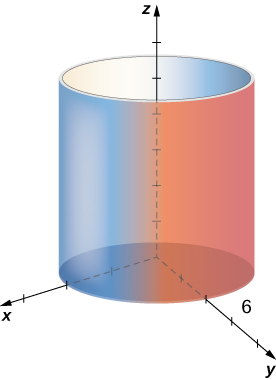
Describe the surface with cylindrical equation
This surface is a cylinder with radius
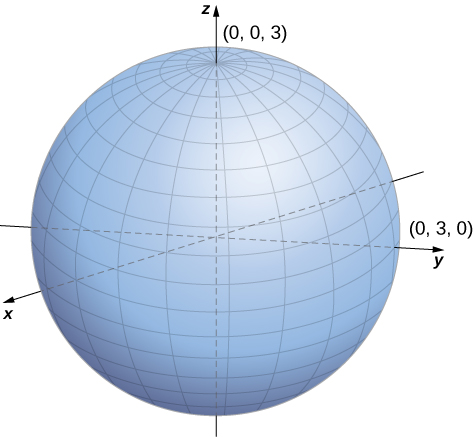
In the Cartesian coordinate system, the location of a point in space is described using an ordered triple in which each coordinate represents a distance. In the cylindrical coordinate system, location of a point in space is described using two distances and an angle measure In the spherical coordinate system, we again use an ordered triple to describe the location of a point in space. In this case, the triple describes one distance and two angles. Spherical coordinates make it simple to describe a sphere, just as cylindrical coordinates make it easy to describe a cylinder. Grid lines for spherical coordinates are based on angle measures, like those for polar coordinates.
In the spherical coordinate system , a point in space ( [link] ) is represented by the ordered triple where

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?