| << Chapter < Page | Chapter >> Page > |
Solve:
|
| |
| Add 6 to each side to undo the subtraction. |
|
| Simplify. |
|
Check the result by substituting into the original equation:
| Substitute for | |
The solution to is
Since makes a true statement, we found the solution to this equation.
All of the equations we have solved so far have been of the form or We were able to isolate the variable by adding or subtracting the constant term. Now we’ll see how to solve equations that involve division.
We will model an equation with envelopes and counters in [link] .
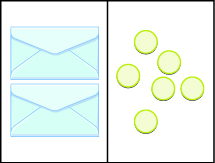
Here, there are two identical envelopes that contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
To determine the number, separate the counters on the right side into groups of the same size. So counters divided into groups means there must be counters in each group (since
What equation models the situation shown in [link] ? There are two envelopes, and each contains counters. Together, the two envelopes must contain a total of counters. So the equation that models the situation is
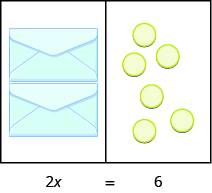
We can divide both sides of the equation by as we did with the envelopes and counters.
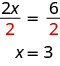
We found that each envelope contains Does this check? We know so it works. Three counters in each of two envelopes does equal six.
[link] shows another example.
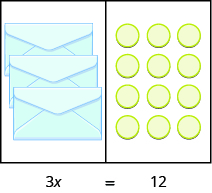
Now we have identical envelopes and How many counters are in each envelope? We have to separate the into Since there must be in each envelope. See [link] .
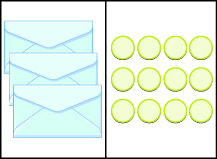
The equation that models the situation is We can divide both sides of the equation by
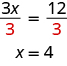
Does this check? It does because
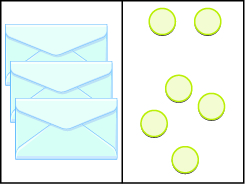
Write an equation modeled by the envelopes and counters, and then solve it.
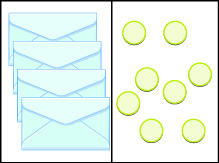
There are
or
unknown values, on the left that match the
on the right. Let’s call the unknown quantity in the envelopes
| Write the equation. |
|
| Divide both sides by 4. |
|
| Simplify. |
|
There are in each envelope.
Write the equation modeled by the envelopes and counters. Then solve it.
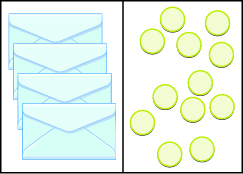
4 x = 12; x = 3
Write the equation modeled by the envelopes and counters. Then solve it.
3 x = 6; x = 2
The previous examples lead to the Division Property of Equality . When you divide both sides of an equation by any nonzero number, you still have equality.
For any numbers and
To isolate
we need to undo multiplication.
|
| |
| Divide each side by 7. |
|
| Simplify. |
|
Check the solution.
| Substitute −7 for x. | |
Therefore, is the solution to the equation.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?