10.2 Use multiplication properties of exponents

Simplify expressions with exponents

Remember that an exponent indicates repeated multiplication of the same quantity. For example, $2^4$ means to multiply four factors of $2,$ so $2^4$ means $2·2·2·2.$ This format is known as exponential notation .

Exponential notation

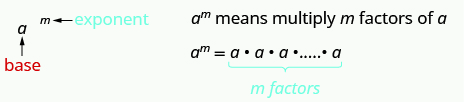
This is read $a$ to the $m^{\mathrm{th}}$ power.

In the expression $a^m,$ the exponent tells us how many times we use the base $a$ as a factor.

Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.

Simplify expressions using the product property of exponents

You have seen that when you combine like terms by adding and subtracting, you need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too. We’ll derive the properties of exponents by looking for patterns in several examples. All the exponent properties hold true for any real numbers, but right now we will only use whole number exponents.

First, we will look at an example that leads to the Product Property.

What does this mean? How many factors altogether?
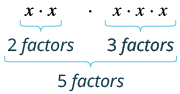So, we have
Notice that 5 is the sum of the exponents, 2 and 3.

The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.

An example with numbers helps to verify this property.

Simplify: $x^5·x^7.$

Solution

	$x^5·x^7$
Use the product property, $a^m·a^n=a^{m+n}.$
Simplify.	$x^{12}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Simplify: $b^4·b.$

Solution

	$b^4·b$
Rewrite, $b=b^1.$	$b^4·b^1$
Use the product property, $a^m·a^n=a^{m+n}.$
Simplify.	$b^5$

Got questions? Get instant answers now!

Got questions? Get instant answers now!