| << Chapter < Page | Chapter >> Page > |
Polygons are all around us. A stop sign is in the shape of an octagon, an eight-sided polygon. The honeycomb of a beehive consists of hexagonal cells. The top of a desk is a rectangle.
In this section, you will learn about similar polygons.
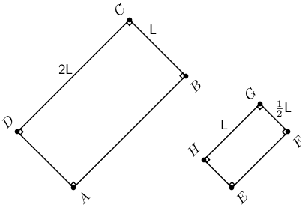
Fill in the table using the diagram and then answer the questions that follow.
| = | =... | ... |
| = | =... | =... |
| = | ... | =... |
If two polygons are similar , one is an enlargement of the other. This means that the two polygons will have the same angles and their sides will be in the same proportion.
We use the symbol to mean is similar to .
Two polygons are similar if:
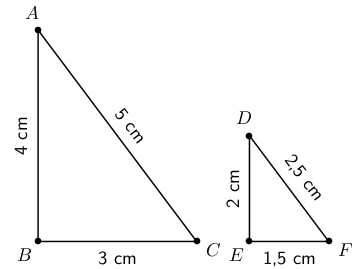
Show that the following two polygons are similar.
We are required to show that the pair of polygons is similar. We can do this by showing that the ratio of corresponding sides is equal and by showing that corresponding angles are equal.
We are given the angles. So, we can show that corresponding angles are equal.
All angles are given to be 90 and
We first need to see which sides correspond. The rectangles have two equal long sides and two equal short sides. We need to compare the ratio of the long side lengths of the two different rectangles as well as the ratio of the short side lenghts.
Long sides, large rectangle values over small rectangle values:
Short sides, large rectangle values over small rectangle values:
The ratios of the corresponding sides are equal, 2 in this case.
Since corresponding angles are equal and the ratios of the corresponding sides are equal the polygons ABCD and EFGH are similar.
If two pentagons ABCDE and GHJKL are similar, determine the lengths of the sides and angles labelled with letters:
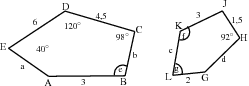
We are given that ABCDE and GHJKL are similar. This means that:
and
We are required to determine the
The corresponding angles are equal, so no calculation is needed. We are given one pair of sides and that correspond. so we know that all sides of are 1,5 times smaller than .
Working in pairs, show that all equilateral triangles are similar.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [ncs]' conversation and receive update notifications?