| << Chapter < Page | Chapter >> Page > |
So far, the main things that we have learned is that shorter pulses require greater bandwidth, and the bandwidth required to faithfully represent atruncated sinusoidal pulse is the reciprocal of the length of the pulse.
Now we will look at the issues involved in using spectral analysis to separate and identify the frequencies of two closely-spaced spectral peaks for apulse composed of the sum of two sinusoids. Once again, we will begin by looking at some results and then discuss the code that produced those results.
The five pulses that we will be working with in this example are shown in Figure 4 . As you can see, these pulses are a little more ugly than the pulses shown in Figure 1 . As you can also see, as was the case in Figure 1 , each pulse appears to be a shorter or longer version of the other pulses in terms of itswaveform.
| Figure 4. Five pulses with two sinusoids each. |
|---|
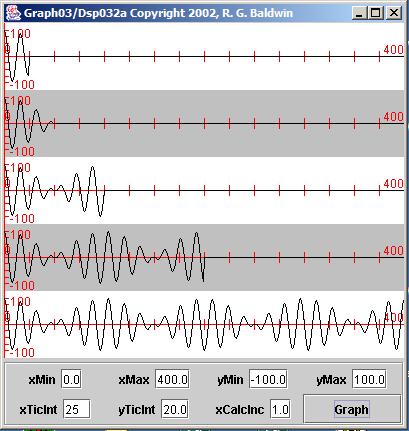 |
The plots in Figure 4 were produced by the program named Dsp032a , which I will briefly discuss later. (A complete listing of the program is shown in Listing 11 near the end of the module.) This program creates and displays pulses identical to those processed by the program named Dsp032 , which I will also briefly discuss later. (A complete listing of the program named Dsp32 is presented in Listing 12 .)
The program creates and displays five separate time series, each 400 samples in length. Each time series contains a pulse and the pulses are differentlengths. As before, each of the pulses shown in Figure 4 is half the length of the pulse below it.
Each pulse consists of the sum of two sinusoids at closely spaced frequencies. The frequencies of the two sinusoids for all pulses are the same.
All frequency values are specified as type double as a fraction of the sampling frequency. The frequencies of the two sinusoids areequidistant from a center frequency of 0.0625 times the sampling frequency.
(Recall that 0.0625 was the frequency of the only sinusoid contained in the pulses shown in Figure 1 and processed by the program named Dsp031 .)
The frequency of one sinusoid is (0.0625 - 2.0/len) times the sampling frequency, where len is the length of the time series containing the pulse. (The value for len is 400 samples in this program.) The frequency of the other sinusoid is (0.0625 + 2.0/len) times the sampling frequency.
The lengths of the five pulses are:
(Note that Figure 4 has tick marks every 25 samples.)
The only new code in this program is the code in the constructor that creates the pulses and stores them in the data arrays. This code consists of fiveseparate for loops, one for each pulse. The code for the first for loop, which is typical of the five, is shown in Listing 6 .
| Listing 6. New code in the the program named Dsp032a. |
|---|
public Dsp032a(){//constructor
//Create the raw datafor(int x = 0;x<len/16;x++){
data1[x]= amp*Math.cos(2*pi*x*freq1)
+ amp*Math.cos(2*pi*x*freq2);}//end for loop
//... code removed for brevity}//end constructor |

Notification Switch
Would you like to follow the 'Digital signal processing - dsp' conversation and receive update notifications?