10.5 Angular momentum and its conservation  (Page 4/7)

Solution for (b)

Rotational kinetic energy is given by

The initial value is found by substituting known values into the equation and converting the angular velocity to rad/s:

The final rotational kinetic energy is

Substituting known values into this equation gives

Discussion

In both parts, there is an impressive increase. First, the final angular velocity is large, although most world-class skaters can achieve spin rates about this great. Second, the final kinetic energy is much greater than the initial kinetic energy. The increase in rotational kinetic energy comes from work done by the skater in pulling in her arms. This work is internal work that depletes some of the skater’s food energy.

There are several other examples of objects that increase their rate of spin because something reduced their moment of inertia. Tornadoes are one example. Storm systems that create tornadoes are slowly rotating. When the radius of rotation narrows, even in a local region, angular velocity increases, sometimes to the furious level of a tornado. Earth is another example. Our planet was born from a huge cloud of gas and dust, the rotation of which came from turbulence in an even larger cloud. Gravitational forces caused the cloud to contract, and the rotation rate increased as a result. (See [link] .)

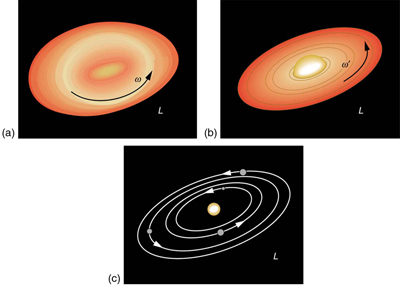
In case of human motion, one would not expect angular momentum to be conserved when a body interacts with the environment as its foot pushes off the ground. Astronauts floating in space aboard the International Space Station have no angular momentum relative to the inside of the ship if they are motionless. Their bodies will continue to have this zero value no matter how they twist about as long as they do not give themselves a push off the side of the vessel.

Section summary

• Every rotational phenomenon has a direct translational analog , likewise angular momentum $L$ can be defined as $L=\mathrm{I\omega }.$
• This equation is an analog to the definition of linear momentum as $p=\text{mv}$ . The relationship between torque and angular momentum is $\text{net}\tau =\frac{\text{Δ}L}{\text{Δ}t}.$
• Angular momentum, like energy and linear momentum, is conserved. This universally applicable law is another sign of underlying unity in physical laws. Angular momentum is conserved when net external torque is zero, just as linear momentum is conserved when the net external force is zero.

Conceptual questions