| << Chapter < Page | Chapter >> Page > |
Additional general information can be obtained from [link] and the expression for a straight line, .
In this case, the vertical axis is , the intercept is , the slope is , and the horizontal axis is . Substituting these symbols yields
A general relationship for velocity, acceleration, and time has again been obtained from a graph. Notice that this equation was also derived algebraically from other motion equations in Motion Equations for Constant Acceleration in One Dimension .
It is not accidental that the same equations are obtained by graphical analysis as by algebraic techniques. In fact, an important way to discover physical relationships is to measure various physical quantities and then make graphs of one quantity against another to see if they are correlated in any way. Correlations imply physical relationships and might be shown by smooth graphs such as those above. From such graphs, mathematical relationships can sometimes be postulated. Further experiments are then performed to determine the validity of the hypothesized relationships.
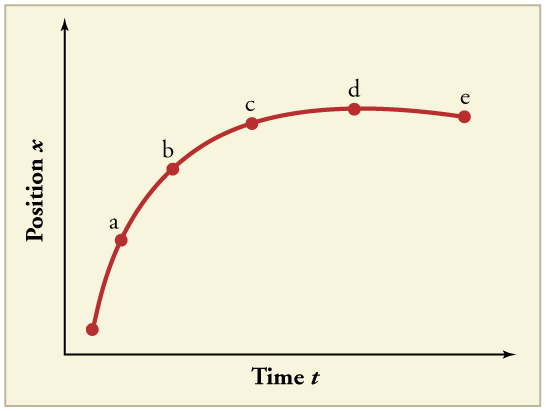
(a) Explain how you can use the graph of position versus time in [link] to describe the change in velocity over time. Identify (b) the time ( , , , , or ) at which the instantaneous velocity is greatest, (c) the time at which it is zero, and (d) the time at which it is negative.
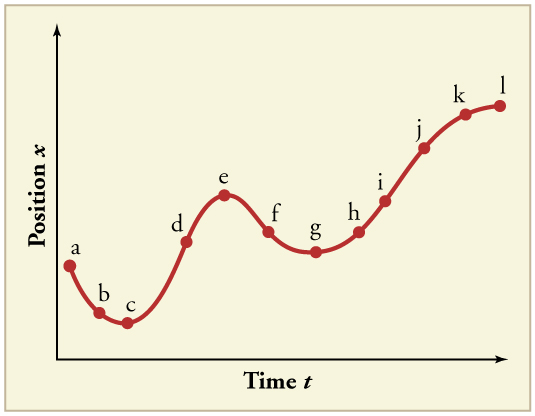
(a) Sketch a graph of velocity versus time corresponding to the graph of displacement versus time given in [link] . (b) Identify the time or times ( , , , etc.) at which the instantaneous velocity is greatest. (c) At which times is it zero? (d) At which times is it negative?
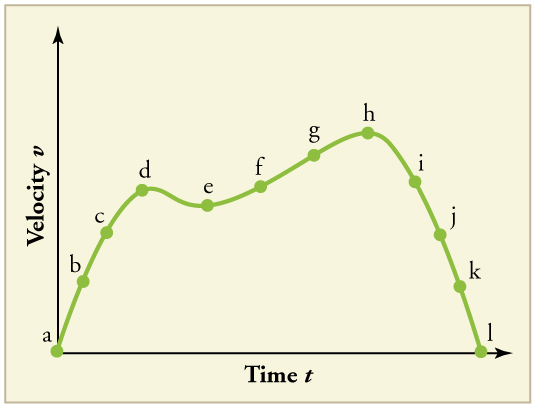
(a) Explain how you can determine the acceleration over time from a velocity versus time graph such as the one in [link] . (b) Based on the graph, how does acceleration change over time?

(a) Sketch a graph of acceleration versus time corresponding to the graph of velocity versus time given in [link] . (b) Identify the time or times ( , , , etc.) at which the acceleration is greatest. (c) At which times is it zero? (d) At which times is it negative?
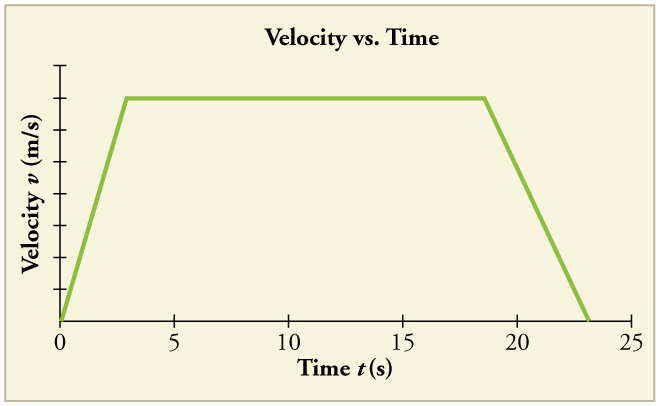
Consider the velocity vs. time graph of a person in an elevator shown in [link] . Suppose the elevator is initially at rest. It then accelerates for 3 seconds, maintains that velocity for 15 seconds, then decelerates for 5 seconds until it stops. The acceleration for the entire trip is not constant so we cannot use the equations of motion from Motion Equations for Constant Acceleration in One Dimension for the complete trip. (We could, however, use them in the three individual sections where acceleration is a constant.) Sketch graphs of (a) position vs. time and (b) acceleration vs. time for this trip.
A cylinder is given a push and then rolls up an inclined plane. If the origin is the starting point, sketch the position, velocity, and acceleration of the cylinder vs. time as it goes up and then down the plane.
Note: There is always uncertainty in numbers taken from graphs. If your answers differ from expected values, examine them to see if they are within data extraction uncertainties estimated by you.
(a) By taking the slope of the curve in [link] , verify that the velocity of the jet car is 115 m/s at . (b) By taking the slope of the curve at any point in [link] , verify that the jet car’s acceleration is .
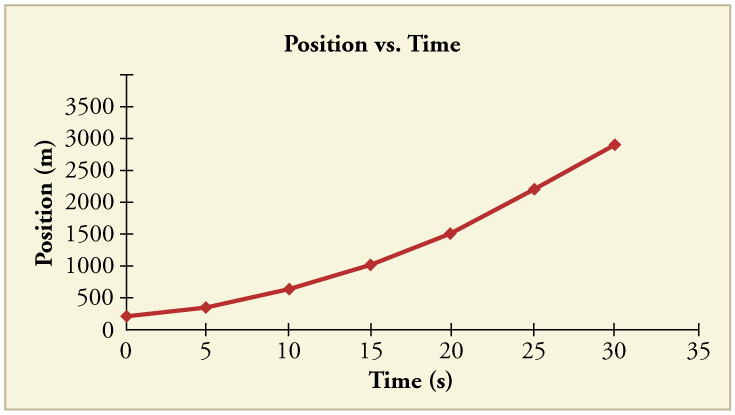
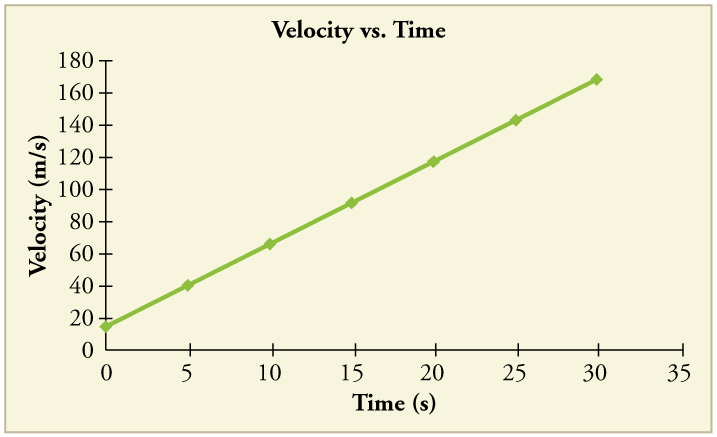
(a)
(b)
Construct the displacement graph for the subway shuttle train as shown in [link] (a). Your graph should show the position of the train, in kilometers, from t = 0 to 20 s. You will need to use the information on acceleration and velocity given in the examples for this figure.
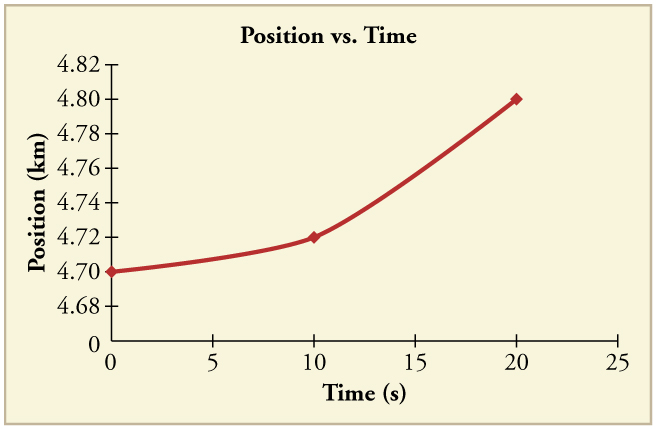

Notification Switch
Would you like to follow the 'Kinematics' conversation and receive update notifications?