0.6 Sorting  (Page 15/20)

One advantage of parallel quicksort over other parallel sort algorithms is that no synchronization is required. A new thread is started as soon as a sublist is available for it to work on and it does not communicate with other threads. When all threads complete, the sort is done.

Other more sophisticated parallel sorting algorithms can achieve even better time bounds. For example, in 1991 David Powers described a parallelized quicksort that can operate in O(log n) time given enough processors by performing partitioning implicitly [1] .

Formal analysis

From the initial description it's not obvious that quicksort takes O(n log n)time on average. It's not hard to see that the partition operation, which simply loops over the elements of the array once, uses Θ(n) time. In versions that perform concatenation, this operation is also Θ(n).

In the best case, each time we perform a partition we divide the list into two nearly equal pieces. This means each recursive call processes a list of half the size. Consequently, we can make only (log n) nested calls before we reach a list of size 1. This means that the depth of the call tree is O(log n). But no two calls at the same level of the call tree process the same part of the original list; thus, each level of calls needs only O(n) time all together (each call has some constant overhead, but since there are only O(n) calls at each level, this is subsumed in the O(n) factor). The result is that the algorithm uses only O(n log n) time.

An alternate approach is to set up a recurrence relation for T(n) factor), the time needed to sort a list of size n. Because a single quicksort call involves O(n) factor) work plus two recursive calls on lists of size n/2 in the best case, the relation would be:

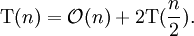
The master theorem tells us that .

In fact, it's not necessary to divide the list this precisely; even if each pivot splits the elements with 99% on one side and 1% on the other (or any other fixed fraction), the call depth is still limited to (100log n), so the total running time is still O(n log n).

In the worst case, however, the two sublists have size 1 and n − 1, and the call tree becomes a linear chain of n nested calls. The ith call does work, and . The recurrence relation is:

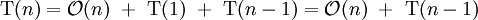
This is the same relation as for insertion sort and selection sort , and it solves to T(n) = Θ(n2).

Randomized quicksort expected complexity

Randomized quicksort has the desirable property that it requires only O(n log n) expected time, regardless of the input. But what makes random pivots a good choice?

Suppose we sort the list and then divide it into four parts. The two parts in the middle will contain the best pivots; each of them is larger than at least 25% of the elements and smaller than at least 25% of the elements. If we could consistently choose an element from these two middle parts, we would only have to split the list at most 2log2n times before reaching lists of size 1, yielding an O(n log n) algorithm.

Unfortunately, a random choice will only choose from these middle parts half the time. The surprising fact is that this is good enough. Imagine that you are flipping a coin over and over until you get k heads. Although this could take a long time, on average only 2k flips are required, and the chance that you won't get k heads after 100k flips is infinitesimally small. By the same argument, quicksort's recursion will terminate on average at a call depth of only 2log2n. But if its average call depth is O(log n), and each level of the call tree processes at most n elements, the total amount of work done on average is the product, O(n log n).