3.5 The least common multiple

We can visualize common multiples using the number line.

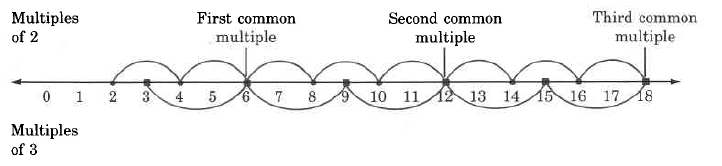
Notice that the common multiples can be divided by both whole numbers.

9 and 12

1. $\begin{array}{c}9=3\cdot 3=3^2\hfill \\ \text{12}=2\cdot 6=2\cdot 2\cdot 3=2^2\cdot 3\hfill \end{array}$

2. The bases that appear in the prime factorizations are 2 and 3.
3. The largest exponents appearing on 2 and 3 in the prime factorizations are, respectively, 2 and 2:

   $2^2$ from 12.

   $3^2$ from 9.

4. The LCM is the product of these numbers.

   LCM $=2^2\cdot 3^2=4\cdot 9=\text{36}$

Thus, 36 is the smallest number that both 9 and 12 divide into without remainders.

90 and 630

1. $\begin{array}{cccc}\mathrm{90}& =& 2\cdot \text{45}=2\cdot 3\cdot \mathrm{15}=2\cdot 3\cdot 3\cdot 5=2\cdot 3^2\cdot 5\hfill & \\ \mathrm{630}& =& 2\cdot \text{315}=2\cdot 3\cdot \text{105}=2\cdot 3\cdot 3\cdot \text{35}\hfill & =2\cdot 3\cdot 3\cdot 5\cdot 7\\ & & & =2\cdot 3^2\cdot 5\cdot 7\hfill \end{array}$

2. The bases that appear in the prime factorizations are 2, 3, 5, and 7.
3. The largest exponents that appear on 2, 3, 5, and 7 are, respectively, 1, 2, 1, and 1:
   • $2^1$ from either 90 or 630.
   • $3^2$ from either 90 or 630.
   • $5^1$ from either 90 or 630.
   • $7^1$ from 630.
4. The LCM is the product of these numbers.

   LCM $=2\cdot 3^2\cdot 5\cdot 7=2\cdot 9\cdot 5\cdot 7=\text{630}$

Thus, 630 is the smallest number that both 90 and 630 divide into with no remainders.

33, 110, and 484

1. $\begin{array}{ccc}\mathrm{33}& =& 3\cdot \mathrm{11}\hfill \\ \mathrm{110}& =& 2\cdot \mathrm{55}=2\cdot 5\cdot \mathrm{11}\hfill \\ \mathrm{484}& =& 2\cdot \mathrm{242}=2\cdot 2\cdot \mathrm{121}=2\cdot 2\cdot \mathrm{11}\cdot \mathrm{11}=2^2\cdot {\mathrm{11}}^2.\hfill \end{array}$

2. The bases that appear in the prime factorizations are 2, 3, 5, and 11.
3. The largest exponents that appear on 2, 3, 5, and 11 are, respectively, 2, 1, 1, and 2:
   • $2^2$ from 484.
   • $3^1$ from 33.
   • $5^1$ from 110
   • ${\text{11}}^2$ from 484.
4. The LCM is the product of these numbers.

   $\begin{array}{ccc}\text{LCM}& =& 2^2\cdot 3\cdot 5\cdot {\mathrm{11}}^2\hfill \\ & =& 4\cdot 3\cdot 5\cdot \mathrm{121}\hfill \\ & =& \mathrm{7260}\hfill \end{array}$

   Thus, 7260 is the smallest number that 33, 110, and 484 divide into without remainders.