| << Chapter < Page | Chapter >> Page > |
All objects have energy. The word energy comes from the Greek word energeia ( ), meaning activity or operation. Energy is closely linked to mass and cannot be created or destroyed. In this chapter we will consider potential and kinetic energy.
The potential energy of an object is generally defined as the energy an object has because of its position relative to other objects that it interacts with. There are different kinds of potential energy such as gravitional potential energy, chemical potential energy, electrical potential energy, to name a few. In this section we will be looking at gravitational potential energy.
Potential energy is the energy an object has due to its position or state.
Gravitational potential energy is the energy of an object due to its position above the surface of the Earth. The symbol is used to refer to gravitational potential energy. You will often find that the words potential energy are used where gravitational potential energy is meant. We can define potential energy (or gravitational potential energy, if you like) as:
where = potential energy measured in joules (J)
m = mass of the object (measured in kg)
g = gravitational acceleration ( )
h = perpendicular height from the reference point (measured in m)
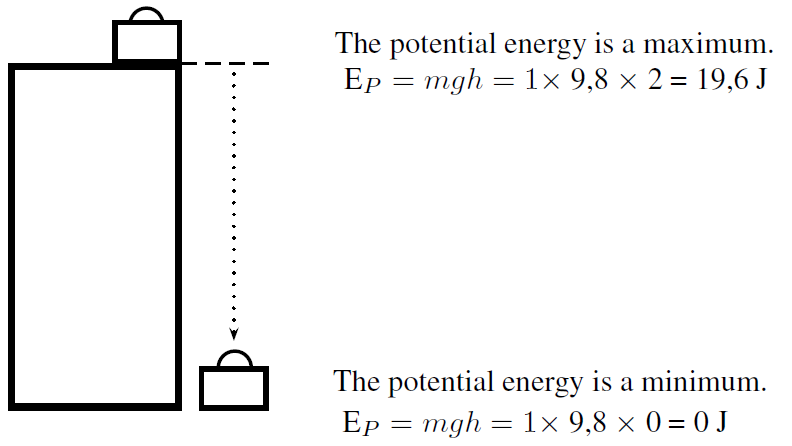
A suitcase, with a mass of , is placed at the top of a high cupboard. By lifting the suitcase against the force of gravity, we give the suitcase potential energy. This potential energy can be calculated using [link] .
If the suitcase falls off the cupboard, it will lose its potential energy. Halfway down the cupboard, the suitcase will have lost half its potential energy and will have only left. At the bottom of the cupboard the suitcase will have lost all it's potential energy and it's potential energy will be equal to zero.
Objects have maximum potential energy at a maximum height and will lose their potential energy as they fall.
A brick with a mass of is lifted to the top of a high roof. It slips off the roof and falls to the ground. Calculate the potential energy of the brick at the top of the roof and on the ground once it has fallen.
All quantities are in SI units.
Since the block is being lifted we are dealing with gravitational potential energy. To work out , we need to know the mass of the object and the height lifted. As both of these are given, we just substitute them into the equation for .

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?