| << Chapter < Page | Chapter >> Page > |
Một trong những công việc quan trọng nhất trong việc phân giải và thiết kế các hệ tự kiểm là mô hình hóa hệ thống. Ở những chương trước, ta đã đưa vào một số phương pháp mô hình hóa hệ thống thông dụng. Hai phương pháp chung nhất là hàm chuyển và phương trình trạng thái. Phương pháp hàm chuyển chỉ có giá trị đối với các hệ tuyến tính, không đổi theo thời gian. Trong khi các phương trình trạng thái, là những phương trình vi phân cấp một có thể dùng mô tả các hệ tuyến tính và cả phi tuyến. Vì trong thực tế, tất cả các hệ vật lý đều phi tuyến trong một vài phạm vi hoạt động. Nên để có thể sử dụng hàm chuyển chuyển và các phương trình trạng thái tuyến tính, hệ thống phải được tuyến tính hoá, hoặc là hoạt động của nó phải được hạn chế trong vùng tuyến tính.
Dù sự phân giải và thiết kế các hệ điều khiển tuyến tính đã được phát triển tốt, nhưng bản sao của nó cho các hệ phi tuyến thì thường rất phức tạp.
Kỹ thuật điều khiển thường phải xác định không chỉ việc làm sao để mô tả chính xác hệ thống một cách toán học, mà còn phải, quan trọng hơn, làm sao để đặt các giả thuyết đúng, và phép tính xấp xỉ (nếu cần thiết) sao cho hệ thống có thể được đặc trưng hóa một cách tương xứng bởi một mô hình toán học tuyến tính.
Thật quan trọng để thấy rằng, kỹ thuật điều khiển hiện đại phải dựa trên sự mô hình hoá hệ thống sao cho vấn đề phân giải và thiết kế có thể phù hợp với các lời giải nhờ máy tính. Như vậy, chủ đích của chương này là:
- Để chứng tỏ sự mô hình hoá toán học của các hệ thông điều khiển và các bộ phận.
- Để chứng tỏ bằng cách nào sự mô hình hoá sẽ dẫn đến các lời giải trên máy tính.
Phương pháp cổ điển để viết các phương trình của mạch điện được đặt trên cơ sở hai định luật về nút và vòng của kirchhoff. Tuy hai định luật này thì đơn giản nhưng các phương trình kết quả thì không tự nhiên đối với máy tính.
Một phương pháp mới để viết các phương trình mạch điện là phương pháp biến trạng thái. Vì các mạch điện trong phần lớn các hệ tự kiểm thì không phức tạp lắm, ta sẽ trình bày ở đây chỉ ở mức độ giới thiệu. Những lý giải chi tiết về các phương trình trạng thái cho mạch điện có thể tìm ở các giáo trình lý thuyết mạch.
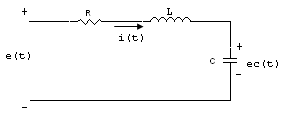
H.5_1.
Xem mạch RLC như hình H.5_1. Phương cách thực hành là xem dòng điện trong cuộn cảm L và điện thế ngang qua tụ C là các biến trạng thái (tức i(t) và ec(t)). Lý do của sự chọn lựa này là vì các biến trạng thái thì liên hệ trực tiếp với bộ phận tích trữ năng lượng của một hệ thống. Trong trường hợp này, cuộn cảm tích trữ động năng và tụ tích trữ thế năng.
Bằng cách chọn i(t) và ec(t) là các biến trạng thái, ta có một sự mô tả hoàn toàn về quá khứ (tức trị giá đầu của chúng) hiện tại và trạng thái tương lai của mạch.
Ta có:
Dòng điện trong tụ C : (5.1)
Điện thế ngang qua L : (5.2)
Các phương trình trạng thái dưới dạng ma trận, được viết:
(5.3)
Thí dụ5_1 : Xem mạch điện như hình H.5_2.

Notification Switch
Would you like to follow the 'Cơ sở tự động học' conversation and receive update notifications?