| << Chapter < Page | Chapter >> Page > |
ĐỘ LINH ĐỘNG VÀ DẪN XUẤT:
Trong chương I, hình ảnh của dải năng lượng trong kim loại đã được trình bày. Theo sự khảo sát trên, dải năng lượng do điện tử chiếm có thể chưa đầy và không có dải cấm cho những năng lượng cao. Nghĩa là điện tử có thể di chuyển tự do trong kim loại dưới tác dụng của điện trường.
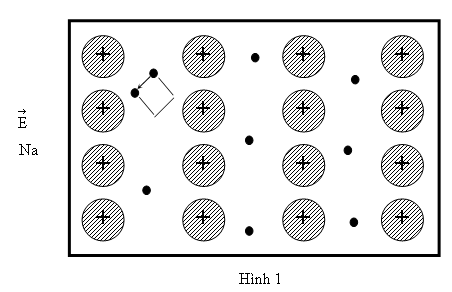
Hình trên vẽ phân bố điện tích trong tinh thể Na. Những chỗ gạch chéo tiêu biểu cho những điện tử ở dải hóa trị có năng lượng thấp nhất, những chỗ trắng chứa những điện tử có năng lượng cao nằm trong dải dẫn điện. Chính những điện tử này là những điện tử không thể nói thuộc hẳn vào một nguyên tử nhất định nào và có thể di chuyển tự do từ nguyên tử này sang nguyên tử khác. Vậy kim loại được coi là nơi các ion kết hợp chặt chẽ với nhau và xếp đều đặn trong 3 chiều trong một đám mây điện tử mà trong đó điện tử có thể di chuyển tự do.
Hình ảnh này là sự mô tả kim loại trong chất khí điện tử. Theo thuyết chất khí điện tử kim loại, điện tử chuyển động liên tục với chiều chuyển động biến đổi mỗi lần va chạm với ion dương nặng, được xem như đứng yên. Khoảng cách trung bình giữa hai lần va chạm được gọi là đoạn đường tự do trung bình. Vì đây là chuyển động tán loạn, nên ở một thời điểm nào đó, số điện tử trung bình qua một đơn vị diện tích theo bất cứ chiều nào sẽ bằng số điện tử qua đơn vị diện tích ấy theo chiều ngược lại. Như vậy , dòng điện trung bình triệt tiêu.
Giả sử, một điện trường được thiết lập trong mạng tinh thể kim loại, ta thử khảo sát chuyển động của một điện tử trong từ trường nầy.
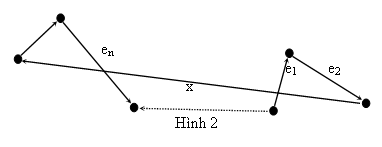
Hình trên mô tả chuyển động của điện tử dưới tácdụng của điện trường . Quỹ đạo của điện tử là một đường gấp khúc vì điện tử chạm vào các ion dương và đổi hướng chuyển động. Trong thời gian t=n lần thời gian tự do trung bình, điện tử di chuyển được một đoạn đường là x. Vận tốc gọi là vận tốc trung bình. Vận tốc này tỉ lệ với điện trường .
Hằng số tỉ lệ gọi là độ linh động của điện tử, tính bằng m2/Vsec.
Điện tích đi qua mỗi đơn vị diện tích trong một đơn vị thời gian được gọi là mật độ dòng điện J.
Ta có: J = n.e.v
Trong đó, n: mật độ điện tử, e: điện tích của một electron
t = -1t = 0S’ SvHình 3Bây giờ, ta xét một điện tích vi cấp S đặt thẳng góc với chiều di chuyển của điện tử. Những điện tử tới mặt S ở thời điểm t=0 (t=0 được chọn làm thời điểm gốc) là những điện tử ở trên mặt S’ cách S một khoảng v (vận tốc trung bình của điện tủ) ở thời điểm t=-1. Ở thời điểm t=+1, những điện tử đi qua mặt S chính là những điện tử chứa trong hình trụ giới hạn bởi mặt S và S’. Điện tích của số điện tử này là q=n.e.v.s, với n là mật độ điện tử di chuyển. Vậy điện tích đi ngang qua một đơn vị diện tích trong một đơn vị thời gian là: J=n.e.v
Nhưng nên
Người ta đặt (đọc là Sigma)
Nên gọi là dẫn xuất của kim loại
Và gọi là điện trở suất của kim loại
Điện trở suất tính bằng m và dẫn suất tính bằng mho/m

Notification Switch
Would you like to follow the 'Điện tử ứng dụng' conversation and receive update notifications?