| << Chapter < Page | Chapter >> Page > |
Die gradiënt van 'n reguitlyngrafiek word bereken met:
vir 2 punte en op die grafiek.
Ons kan nou die gemiddelde gradiënt tussen 2 punte en bepaal, selfs al word hulle gedefinieer deur 'n funksie wat nie 'n reguitlyn is nie, met:
Dit is dieselfde as [link] .
Voltooi die tabel deur die gemiddelde gradiënt oor die aangeduide intervalle te bereken vir die funksie . Let daarop dat ( ; ) die koördinate is van die eerste punt en dat ( ; ) die koördinate is van die tweede punt. So, vir AB is ( ; ) die koördinate van punt A en ( ; ) is die koördinate van punt B.
| A-B | |||||
| A-C | |||||
| B-C |
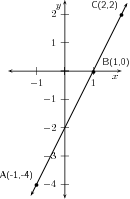
Wat let jy op van die gradiënte oor elke interval?
Die gemiddelde gradiënt van 'n reguitlynfunksie is dieselfde oor enige twee intervalle in die funksie.
Vul die tabel in deur die gemiddelde gradiënt oor die aangeduide intervalle te bereken vir die funksie :
| A-B | |||||
| B-C | |||||
| C-D | |||||
| D-E | |||||
| E-F | |||||
| F-G |
Wat let jy op van die gemiddelde gradiënt oor elke interval? Wat kan jy sê oor die gemiddelde gradiënte tussen A en D in vergelyking met die gemiddelde gradiënte tussen D en G?
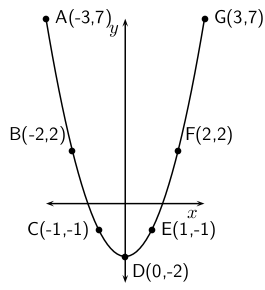
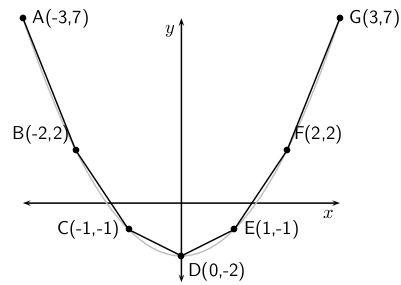
Die gemiddelde gradiënt van 'n paraboliese funksie hang af van die interval en is die gradiënt van 'n reguitlyn wat deur die betrokke punte op daardie interval loop.
Byvoorbeeld, in [link] is die verskeie punte verbind deur reguitlyne. Die gemiddelde gradiënte tussen die betrokke punte is dan die gradiënte van die reguitlyne wat deur daardie punte loop.
Gegee, die vergelyking van 'n kromme en twee punte ( ; ):
Vind die gemiddelde gradiënt van die kromme tussen die punte en .
Merk die punte as volg:
om dit makliker te maak om die gradiënt te bereken.
Ons gebruik die vergelyking van die kromme om die -waarde van die kromme by en te vind.
Die gemiddelde gradiënt tussen en op die kromme is 0.

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?