| << Chapter < Page | Chapter >> Page > |
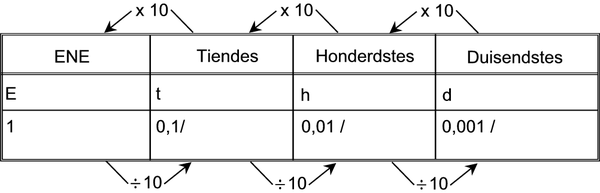
Bv.
| E | t | h | d |
| X | |||
| X | X | ||
| X | X | X | |
| X | X | X | X |
1.1
| E | t | h | d |
| X | |||
| X | X | ||
| X | X | ||
| X | X | ||
| X | X | X | |
| X | X | X |
1.2
| E | t | h | d |
| x | |||
| x | |||
| x | |||
| x | x | ||
| x | x | x | |
| x | x | x |
1.3
| E | t | h | d |
| x | |||
| x | |||
| x | x | ||
| x | x | ||
| x | x | x | |
| x | x | x | |
| x | x | x |
2. Kan jy bogenoemde as gemengde getalle / gewone breuke skryf?
1. Kleur net die sakke wat swaarder as 1,5 kg weeg, in:
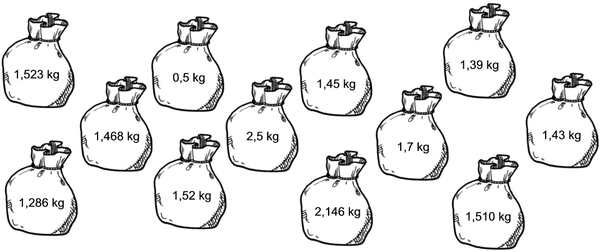
2. In module 1 het ons baie oor die waarde en plekwaarde van syfers gesels. (Onthou jy nog?) Kyk goed na die volgende getalle en skryf dan die waarde van elke onderstreepte syfer neer:
Bv. 3,76 8 :
2.1: 4,2 3 1 :
2.2: 8, 9 23 :
2.3: 289, 7 :
2.4: 2 1,38 :
2.5: 57,23 6 :
2.6: 9,8 9 7 :
3. Vergelyk die volgende getalle met mekaar. Omkring die kleinste een.
Wenk: jy kan dit verander na gewone breuke / gemengde getalle as jy wil – so sal jy dalk makliker die antwoord kry.
3.1: 0,6 ; 0.06 ; 0,006
3.2: 3,2 ; 0,32 ; 0,032
3.3: 1,101 ; 1,111 ; 1,110
Kopkrapper!
Hoe lyk een agste ( ) as ’n desimale breuk? .......................
En ?....................... En ? ........................ En ? .......................
Kan jy as ’n desimale breuk skryf? ..........................
Hoe lyk as ’n desimale breuk? .........................
Verduidelik hoe jy jou antwoorde gekry het SONDER om ’n sakrekenaar te gebruik!
| Leeruitkomstes(LUs) |
| LU 1 |
| Getalle, Verwerkings en VerwantskappeDie leerder is in staat om getalle en die verwantskappe daarvan te herken, te beskryf en voor te stel, en om tydens probleemoplossing bevoeg en met selfvertroue te tel, te skat, te bereken en te kontroleer. |
| Assesseringstandaarde(ASe) |
| Dit is duidelik wanneer die leerder: |
| 1.3 die volgende getalle herken en voorstel, sodat dit beskryf en vergelyk kan word: |
| 1.3.3 desimale breuke in terme van 0,5; 1,5; 2,5, ensovoorts, in konteks van meting; |
| 1.5 ekwivalente vorms van die bogenoemde getalle herken en gebruik, insluitend: |
|
1.6 probleme in kontekste oplos, insluitend kontekste wat gebruik kan word om ‘n bewustheid van ander leerareas, asook van menseregte-, sosiale, ekonomiese en omgewingskwessies, te bevorder, soos:
|
1.8 deur geskikte bewerkings skat en bereken vir die oplossing van probleme in verband met die volgende te kies en gebruik:
|
| 1.9 hoofberekenings uitvoer wat die volgende behels:1.9.1 optelling en aftrekking;1.9.2 vermenigvuldiging van heelgetalle tot minstens 10 x 10; |
| 1.10 ‘n verskeidenheid tegnieke gebruik om sowel skriftelike as hoofberekeninge met heelgetalle te doen, insluitend:1.10.2 opbou en afbreek van getalle;1.10.5 gebruik van ‘n sakrekenaar; |
| 1.11 ‘n verskeidenheid strategieë gebruik om oplossings te kontroleer en die redelikheid van oplossings te beoordeel. |
| LU 5 |
| DatahanteringDie leerder is in staat om data te versamel, op te som, voor te stel en krities te ontleed om gevolgtrekkings en voorspellings te maak en om toevallige variasies te interpreteer en te bepaal. |
| Dit is duidelik wanneer die leerder: |
| 5.3 data organiseer en aanteken deur tellings en tabelle te gebruik. |
1. 1.1: = 0,36
1.2: = 1,07
1.3: = 3,6 / 3,60
1.4: = 42,85
1.5: = 47,03
KOPKRAPPER
1. 0,03
2. 0,09
3. 0,4
4. 0,8
5. 0,37
6. 0,59
Net een syfer na die komma.
Sakrekenaar wys nie die laaste nul nie.
AKTIWITEIT 2
1.
A B C D

AKTIWITEIT 4
1. 1.1>
1.2>
1.3<
1.4<
1.5<
1.6 =
KOPKRAPPER
a) 0,75
AKTIWITEIT 6
1. 1.1: 5,026
2. 2.1: 5
2.2: 2
2.3:
AKTIWITEIT 7
1. 1,523; 1,52; 2,5; 2,146; 1,7; 1,510; 3,5
2. 2.1
2.2
2.3
2.4 20
2.5
2.6
3. 3.1: 0,006
3.2: 0,032
3.3: 1,101
KOPKRAPPER
0,125; 0,375; 0,625; 0,875
0,448
0,7
Verander noemer na 1 000 (ekwivalente breuke)

Notification Switch
Would you like to follow the 'Wiskunde graad 5' conversation and receive update notifications?