| << Chapter < Page | Chapter >> Page > |
A fair coin is flipped 15 times. Each flip is independent. What is the probability of getting more than ten heads? Let X = the number of heads in 15 flips of the fair coin. X takes on the values 0, 1, 2, 3, ..., 15. Since the coin is fair, p = 0.5 and q = 0.5. The number of trials is n = 15. State the probability question mathematically.
P ( x >10)
A fair, six-sided die is rolled ten times. Each roll is independent. You want to find the probability of rolling a one more than three times. State the probability question mathematically.
P ( x >3)
Approximately 70% of statistics students do their homework in time for it to be collected and graded. Each student does homework independently. In a statistics class of 50 students, what is the probability that at least 40 will do their homework on time? Students are selected randomly.
a. This is a binomial problem because there is only a success or a __________, there are a fixed number of trials, and the probability of a success is 0.70 for each trial.
a. failure
b. If we are interested in the number of students who do their homework on time, then how do we define X ?
b.
X = the number of statistics students who do their homework on time
d. What is a "failure," in words?
d. Failure is defined as a student who does not complete his or her homework on time.
The probability of a success is
p = 0.70. The number of trials is
n = 50.
f. The words "at least" translate as what kind of inequality for the probability question P ( x ____ 40).
f. greater than or equal to (≥)
The probability question is
P (
x ≥ 40).
Sixty-five percent of people pass the state driver’s exam on the first try. A group of 50 individuals who have taken the driver’s exam is randomly selected. Give two reasons why this is a binomial problem.
This is a binomial problem because there is only a success or a failure, and there are a definite number of trials. The probability of a success stays the same for each trial.
X ~ B ( n , p )
Read this as " X is a random variable with a binomial distribution." The parameters are n and p ; n = number of trials, p = probability of a success on each trial.
It has been stated that about 41% of adult workers have a high school diploma but do not pursue any further education. If 20 adult workers are randomly selected, find the probability that at most 12 of them have a high school diploma but do not pursue any further education. How many adult workers do you expect to have a high school diploma but do not pursue any further education?
Let X = the number of workers who have a high school diploma but do not pursue any further education.
X takes on the values 0, 1, 2, ..., 20 where n = 20, p = 0.41, and q = 1 – 0.41 = 0.59. X ~ B (20, 0.41)
Find P ( x ≤ 12). P ( x ≤ 12) = 0.9738. (calculator or computer)
Go into 2 nd DISTR. The syntax for the instructions are as follows:
To calculate (
x = value): binompdf(
n ,
p , number) if "number" is left out, the result is the binomial probability table.
To calculate
P (
x ≤ value): binomcdf(
n ,
p , number) if "number" is left out, the result is the cumulative binomial probability table.
For this problem: After you are in 2
nd DISTR, arrow down to binomcdf. Press ENTER. Enter 20,0.41,12). The result is
P (
x ≤ 12) = 0.9738.
If you want to find P ( x = 12), use the pdf (binompdf). If you want to find P ( x >12), use 1 - binomcdf(20,0.41,12).
The probability that at most 12 workers have a high school diploma but do not pursue any further education is 0.9738.
The graph of X ~ B (20, 0.41) is as follows:
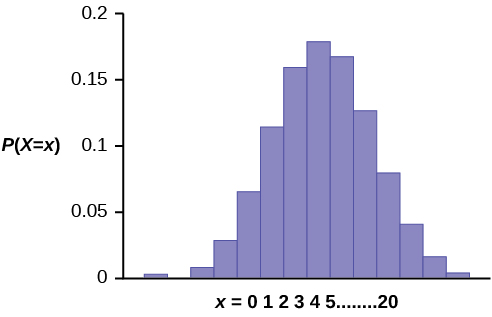
The y -axis contains the probability of x , where X = the number of workers who have only a high school diploma.
The number of adult workers that you expect to have a high school diploma but not pursue any further education is the mean, μ = np = (20)(0.41) = 8.2.
The formula for the variance is σ
2 =
npq . The standard deviation is
σ =
.
σ =
= 2.20.

Notification Switch
Would you like to follow the 'Introductory statistics' conversation and receive update notifications?