| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
So far we have explored addition, subtraction, and multiplication. Now let’s consider division. Suppose you have the cookies in [link] and want to package them in bags with cookies in each bag. How many bags would we need?

You might put cookies in first bag, in the second bag, and so on until you run out of cookies. Doing it this way, you would fill bags.

In other words, starting with the cookies, you would take away, or subtract, cookies at a time. Division is a way to represent repeated subtraction just as multiplication represents repeated addition.
Instead of subtracting repeatedly, we can write
We read this as twelve divided by four and the result is the quotient of and The quotient is because we can subtract from exactly times. We call the number being divided the dividend and the number dividing it the divisor . In this case, the dividend is and the divisor is
In the past you may have used the notation , but this division also can be written as In each case the is the dividend and the is the divisor.
To represent and describe division, we can use symbols and words.

Translate from math notation to words.
ⓐ ⓑ ⓒ
Translate from math notation to words:
ⓐ ⓑ ⓒ
Translate from math notation to words:
ⓐ ⓑ ⓒ
As we did with multiplication, we will model division using counters. The operation of division helps us organize items into equal groups as we start with the number of items in the dividend and subtract the number in the divisor repeatedly.
Model the division:
To find the quotient we want to know how many groups of are in
Model the dividend. Start with
counters.

The divisor tell us the number of counters we want in each group. Form groups of
counters.
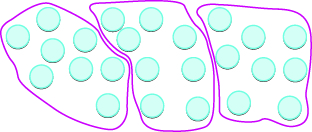
Count the number of groups. There are groups.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?