| << Chapter < Page | Chapter >> Page > |
2.3 Neem twee lang stroke en twee kort stroke en kyk watter verskillende vierhoekige vorms jy kan maak. Toets elke vierhoekige vorm om te sien of dit moontlik is om die vorm te verander wanneer jy liggies aan verskillende hoeke trek. Jy behoort vorms soos die volgende te kry:
 |
| a) die _____________________ |
 |
| b) ‘n parallelogram |
 |
| c) 'n trapesium |
 |
| d) ‘n __________________ |
Probeer nog meer vierhoekige vorms vorm. Al die sye mag verskillende lengtes hê.
2.4 Kan die vierhoekige vorms verander word deur liggies aan die hoeke te trek?
2.5 Hoe sou jy hierdie verandering kon verhoed?
Vierhoekige vorms het vier reguit kante en is nie stewig nie.
3. Indiwiduele werk. Gebruik die vorms op die volgende bladsy, jou potlood, liniaal en 'n skêr om die volgende te doen:
3.1 Verander elke driehoek in 'n seshoekige vorm (seshoek of heksagoon) deur die bestaande hoek af te knip. Knip die seshoeke uit en plak hulle in die raam hier onder. (Hulle hoef nie reëlmatige seshoeke te wees nie; die lengtes van die kante mag maar verskil, maar daar moet ses kante wees.)
3.2 Verander elke vierkantige vorm in 'n agtkantige vorm (oktogoon) deur die hoeke af te knip. (Die agthoek hoef nie reëlmatig te wees nie; die lengtes van die kante mag verskil, maar daar moet agt kante wees.) Knip hierdie vorms uit en plak hulle in die raam hier onder.
V orms om uit te knip:
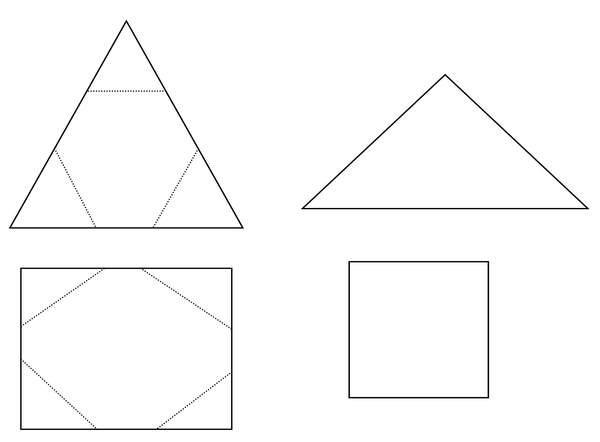
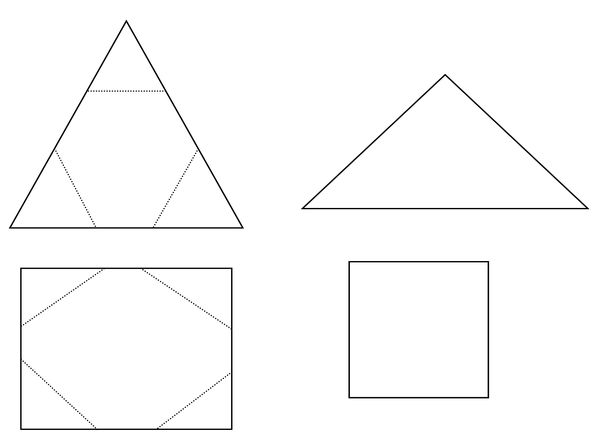
N ie vir uitknip nie:
| 'n Konvekse vorm lyk so: |
 |
| Die konvekse agtkant – die punte wys almal na "buite". |
| 'n Konkawe vorm lyk so: |
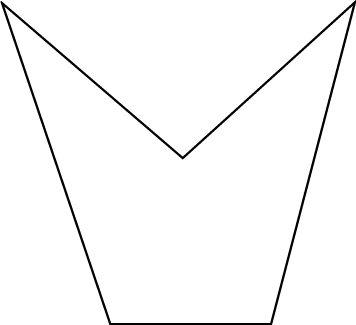 |
| Die konkawe agtkant – daar is steeds vyf kante, maar een punt wys "na binne”. |
4. Indiwiduele werk: Gebruik die geruite papier op die res van hierdie bladsy om een van elk van die volgende vorm te maak en kleur hulle in:
(Die vorms se kante mag verskil - hulle hoef nie reëlmatig te wees nie.)
5. Doen die volgende op die kolletjiespapier:
Voorbeeld:
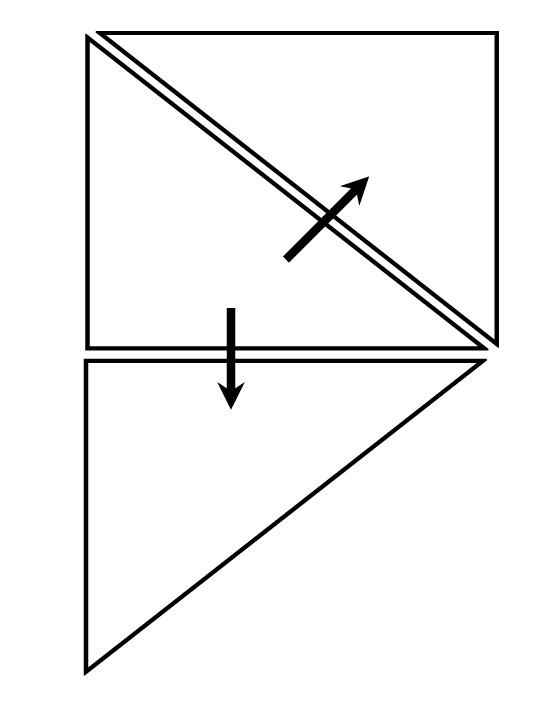
Hier is 'n spasie gelaat om jou te wys hoe die driehoek omgekeer kan word. Onthou dat daar nie spasies mag wees wanneer jy klaar is nie.
My teëlpatroon met driehoeke:

5.3 Maak 'n teëlpatroon met 'n ander driehoek:

5.4 Verbeel jou dat jou reghoek 'n vloerteël is. Oortrek nou die area binne die raam met reghoeke wat identies is aan die een wat jy geteken het. Jy moet geen spasies laat nie en daar mag geen oorvleueling wees nie, maar jy mag jou teëltjie omdraai.
My teëlpatroon met reghoeke:

5.5 Teëlpatroon met vierkante:

5.6 Maak 'n teëlpatroon met ander vierhoeke, bv. vlieërvorms of parallelogramme:

5.7 Gebruik die geruite papier op die volgende bladsy om te kyk watter ander veelhoeke gebruik kan word om die vloer te dek, sonder om spasies te laat en oorvleueling te gebruik, bv. reëlmatige vyfhoeke; reëlmatige seshoeke; reëlmatige agthoeke.
RUITPAPIER (vierkantige blokkies) vir te Ë lpatrone
5.8 IS DIE VOLGENDE PATRONE VOORBEELDE VAN TESSELLASIE?
Skryf ja of nee en verduidelik dan jou antwoord.
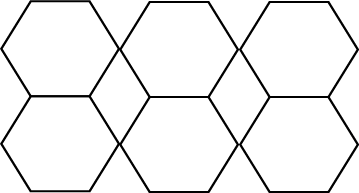
a) __________ Verduidelik jou antwoord: ______________ .
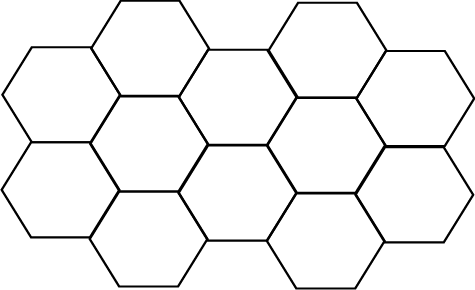
b)___________ Verduidelik jou antwoord: __________________ .
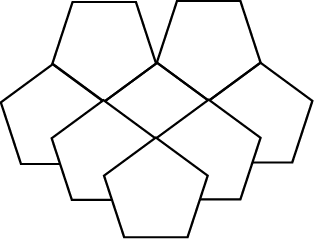
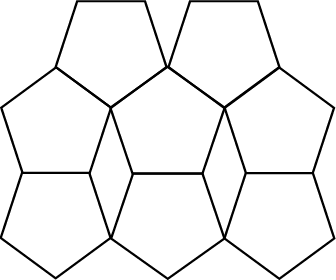
c) . Verduidelik jou antwoord:
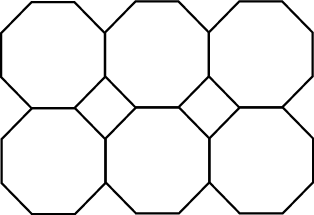
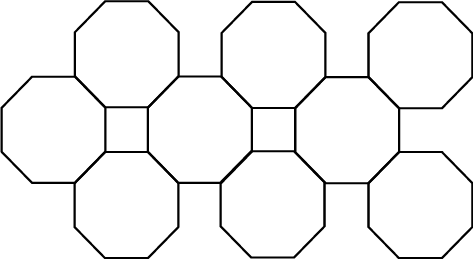
d) . Verduidelik jou antwoord:
| LU 3 |
| Ruimte en VormDie leerder is in staat om eienskappe en verwantskappe tussen tweedimensionele vorms en driedimensionele voorwerpe in 'n verskeidenheid oriëntasies en posisies te beskryf en voor te stel. |
| Dit is duidelik wanneer die leerder: |
3.2 tweedimensionele vorms en driedimensionele voorwerpe uit die omgewing volgens meetkundige eienskappe beskryf, sorteer en vergelyk, insluitend:
|
| 3.3 tweedimensionele vorms en driedimensionele voorwerpe wat in hierdie graad bestudeer word ondersoek en vergelyk (alleen en/of as ‘n lid van ‘n groep of span) volgens die bostaande eienskappe deur die volgende te doen: |
|
|
| 3.4 die simmetrie-lyne in tweedimensionele vorms, insluitend dié wat in die natuur en in kulturele kunsvorms voorkom, herken en beskryf; |
| 3.5 tweedimensionele vorms, driedimensionele voorwerpe en patrone van meetkundige voorwerpe en vorms (bv. tangramme) met die klem op teëling (tessellasie) en lynsimmetrie skep; |
| 3.6 natuurlike en kulturele tweedimensionele vorms en driedimensionele voorwerpe en patrone na aanleiding van meetkundige eienskappe herken en beskryf; |
| 3.7 die verskille in die voorkoms van 'n voorwerp wat in verskillende posisies gehou word, beskryf; |
AKTIWITEIT 1: vergelyking van 2-D fatsoene
(a) Nee
(b) Nee
(c) Nee
(d) Nee
1.2 Praktiese werk
1.3 3
1.4 reguit
1.5 styf / rigied
2. Vierkantige fatsoene
2.1 ja
2.2 ja
2.3 (a) reghoek
(d) vlieër-vormig
2.4 ja
2.5 Voeg een diagonaal in (verbind twee teenoorstaande hoeke met 'n strook karton van die regte lengte en met papierspelde.)
3.1 Prakties: knip en plak
3.2 Prakties: knip en plak
4.1 tot 4.6 Eie werk op geruite papier.
5.1 tot 5.6 Eie werk op gestippelde papier.
5.7 Eie teëlpatroon op geruite papier.
5.8 (a) Nee; daar is spasies tussen die seshoeke, maar Ja, as twee fatsoene toelaatbaar is; die seshoeke en diamantfatsoene dek die area.
(b) Ja, die fatsoen dek die area.
(c) Nee; daar is spasies in die eerste diagram; in die tweede een is daar oorvleueling.
(d) en (e) Ja, as twee fatsoene toelaatbaar is. In dié geval dek 'n aghoek en vierkante die area; agthoeke alleen kan nie so gerankskik word dat die hele area gedek word nie.

Notification Switch
Would you like to follow the 'Wiskunde graad 4' conversation and receive update notifications?