| << Chapter < Page | Chapter >> Page > |
3.2 Count on in 3’s from 0 to 36. Count backwards in 3s from 36 to 0.
3.3 Count on in 5’s from 375 to 425. Count backwards in 5s from 545 to 485.
3.4 Count on in 10’s from 950 to 1 020. Count backwards in 10s from 950 to 840.
3.5 Count on in 25’s from 625 to 1 000. Count backwards in 25s from 975 to 675.
3.6 Count on in 50’s from 550 to 1 050. Count backwards in 50s from 750 to 350.
3.7 Count in hundreds from 400 to 1 100. Count backwards in 100s from 1 000 to 0.
4. COUNTING FORWARDS AND BACKWARDS (Individually):
5. COUNTING WITH LARGER NUMBERS (Oral individual work):
5.1 Count on in 2s from 9 980 to 10 000. Count backwards in 2s from 5 010 to 4 990.
5.2 Count on in 3s from 8 982 to 9 000. Count backwards in 3s from 1 836 to 1 800.
5.3 Count on in 5s from 4 870 to 5 015. Count backwards in 5s from 9 125 to 8 980.
5.4 Count on in 10s from 8 960 to 9 020. Count backwards in 10s from 5 100 to 4 980.
5.5 Count on in 25s from 7 625 to 7 750. Count backwards in 25s from 10 000 to 9 875.
5.6 Count on in 50s from 8 250 to 8 500. Count backwards in 50s from 9 750 to 9 500.
5.7 Count on in hundreds from 5 400 to 6 000. Count backwards in 100s from 7 000 to 6 000
WRITTEN WORK.
Now use your calculator as an investigative tool and complete the written work:
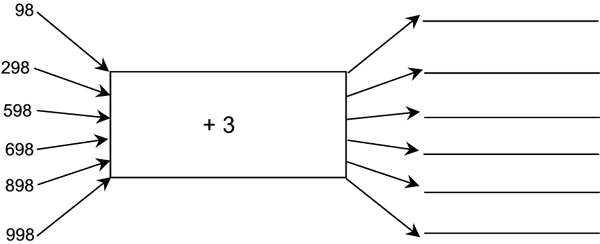
6. FLOW DIAGRAMS :
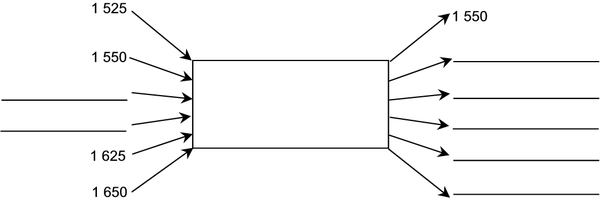
7. A DIFFERENT FLOW DIAGRAM:
8. MORE LARGE NUMBERS
Try to programme your calculator it to “count on” or to “count back” as necessary: Complete the following sequences. Remember, you may use your calculator if you wish.
8.1 10 000; 9 998; 9 996; , , ,
8.2 1 950; 1 960; 1970; , , ,
8.3 9 450; 9 550; 9 650; 9 750; , , ,
8.4 8 825; 8 820; 8 815; , , , ,
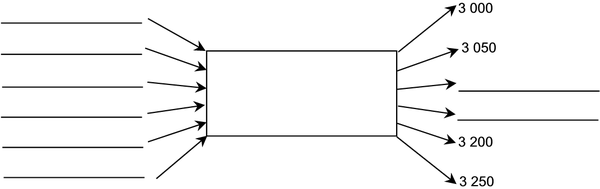
9. LARGER NUMBERS IN A FLOW DIAGRAM:
10. COUNTING IN INTERVALS OF FOUR

Check with a friend, and, if necessary, a calculator.
| Learning outcomes(LOs) |
| LO 1 |
| Numbers, Operations and RelationshipsThe learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems. |
| Assessment standards(ASs) |
| We know this when the learner: |
| 1.1 count forwards and backwards in a variety of intervals (including 2s; 3s; 5s; 10s; 25s; 50s and 100s) between 0 and 10 000; |
| 1.2 describes and illustrates various ways of counting in different cultures (including local) throughout history; |
| 1.3 recognizes and represents the following numbers in order to describe and compare them:1.3.1 whole numbers to at least 4-digit numbers; |
| 1.4 recognizes the place value of digits in whole numbers to at least 4-digit numbers; |
| 1.6 solves problems in context including contexts that may be used to build awareness of other Learning Areas, as well as human rights, social, economic and environmental issues such as:1.6.1 financial (including buying and selling, and simple budgets); |
1.7 solves problems that involve:
|
1.8 estimates and calculates by selecting and using operations appropriate to solving problems that involve:
|
1.9 performs mental calculations involving: addition and subtraction:
|
1.10 uses a range of techniques to perform written and mental calculations with whole numbers including:
|
| 1.11 uses a range of strategies to check solutions and judge the reasonableness of solutions. |
Memorandum
COUNTING IN THE EVERYDAY WORLD
3. COUNTING FORWARDS AND BACKWARDS
3.1 186; 188; 190; 192; 194; 196; 198; 200; 202; 204
206; 204; 202; 200; 198; 196; 194;
3.2 0; 3; 6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36
36; 33; 30; 27; 24; 21; 18; 15; 12; 9; 6; 3; 0
3.3 375; 380; 385; 390; 395; 400; 405; 410; 415; 420; 425
545; 540; 535; 530; 525; 520; 515; 510; 505; 500; 495; 490; 485;
3.4 950; 960; 970; 980; 990; 1 000; 1 010; 1 020
950; 940; 930; 920; 910; 900; 890; 880; 870; 860; 850; 840
3.5 625; 650; 675; 700; 725; 750; 775; 800; 825; 850; 875 900; 925; 950; 975; 1 000
975; 950; 925; 900; 875; 850; 825; 700; 775; 750; 725; 600; 675
3.6 500; 550; 600; 650; 700; 750; 800; 850; 900; 950;
1 000; 1 050
750; 700; 650; 600; 550; 500; 450; 400; 350
3.7 400; 500; 600; 700; 800; 900; 1 000; 1 100
1 000; 900; 800; 700; 600; 500; 400; 300; 200; 100; 0
4. COUNTING: (practice)
5. COUNTING WITH LARGER NUMBERS (Oral individual work; control with a calculator if necessary.)
5.9 980; 9 982; 9 984; 9 986; 9 988; 9 990; 9 992; 9 994; 9 996; 9 998; 10 000
5 010; 5 008; 5 006; 5 004; 5 002; 5 000; 4 998; 4 996; 4 994; 4 992; 4 990
5.2 8 982; 8 985; 8 988; 8 991; 8 994; 8 997
5.2 (cont.) 1 836; 1 833; 1830; … 1 800
5.3 4 870; 4 875; 4 880l; … 5 015
9 125; 9 120; 9115; … 8 980
5.4 8 960; 8 970; 8 980; … 9 020
5 100; 5 090; 5080; … 4 980
5.5 7 625; 7650; 7675; … 7 750
10 000; 9 975; 9 950; … 9 870
5.6 8 250; 8 300; 8 350; … 8 500
9 750; 9 700; 9 650; … 9 500
7 000; 6 900; 6 800; …6 000
Flow Diagrams
6. FLOW DIAGRAMS
6.1
98 + 3 = 101
298 + 3 = 301
598 + 3 = 601
698 + 3 = 701
898 + 3 = 901
998 + 3 = 1001
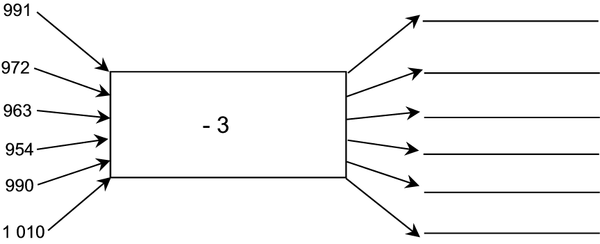
6.2
991 – 3 = 988
972 – 3 = 969
963 – 3 = 960
954 – 3 = 951
990 – 3 = 987
1 010 – 3 = 1 007
7.
1 525 + 25 = 1 550
1 550 + 25 = 1 575
1 575 + 25 = 1 600
1 600 + 25 = 1 625
1 625 + 25 = 1 650
1 650 + 25 = 1 675
8. MORE LARGE NUMBERS
3.1 9 994; 9 992; 9 990; 9 988
3.2 1 980; 1 990; 2 000; 2 010
3.3 9 850; 9950; 10 050; 10 150
3.4 8 810; 8 805; 8 800; 8 795
9. LARGER NUMBERS IN A FLOW DIAGRAM
2 950 + 50 = 3 000
3 000 + 50 = 3 050
3 050 + 50 = 3 100
3 100 + 50 = 3 150
3 200 + 50 = 3 250
10.
The only numbers not encircled are:
1 998
9 998
9 545
7 894
7 898

Notification Switch
Would you like to follow the 'Mathematics grade 4' conversation and receive update notifications?