| << Chapter < Page | Chapter >> Page > |
1.
1.1 Lyn ewe ver middelpunt gebrek
2.
2.1 180
2.2 1
2.3 360
‘n Kykie na sirkels
1. Kyk goed na die skets en beantwoord dan die vrae:
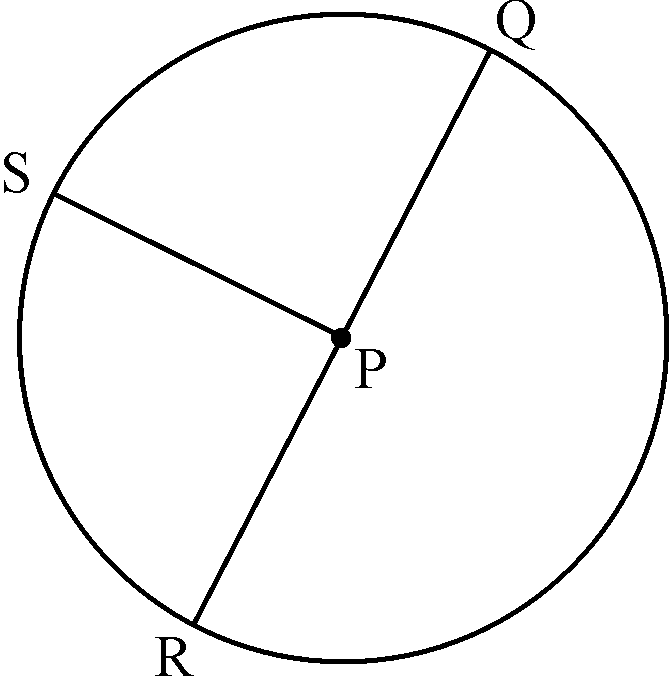
RQ = Middelyn
SP = Straal
1.1 Wat is ‘n sirkel?
_____________________________________________________________________
1.2 Waar, in ons alledaagse lewe, kry ons met sirkels te doen?
_____________________________________________________________________
_____________________________________________________________________
2. Beantwoord die volgende vrae:
2.1 Hoeveel middellyne kan ‘n sirkel hê? ___________________________
2.2 Hoeveel middelpunte kan ‘n sirkel hê? __________________________
2.3 Hoeveel strale (radius) kan ‘n sirkel hê?__________________________
3. Gebruik jou passer en trek ‘n sirkel met ‘n:
3.1 straal van 30 mm
3.2 middellyn van 80 mm
HET JY GEWEET?
Ons kan pragtige patrone met sirkels trek! Die patroon hieronder word “Paisley” genoem en word op klere of stukke lap gebruik.
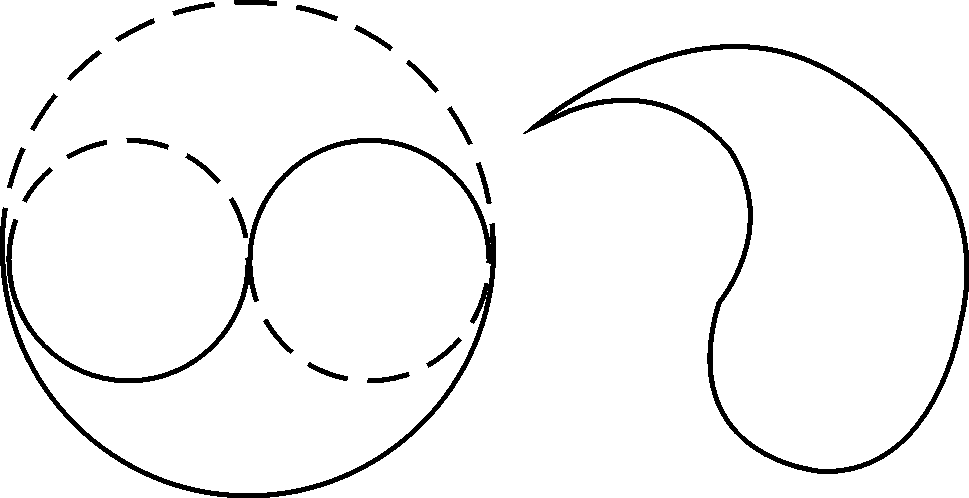
4. Kan jy sien hoe die patroon geteken is? Probeer dit self!
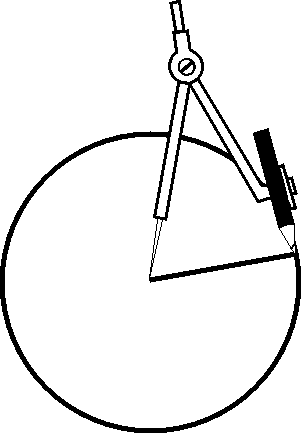
5. Volg die volgende stappe en gebruik dan hierdie metode om die volgende patrone te teken. Jou opvoeder sal die nodige folio verskaf:
Teken ‘n sirkel
Gebruik dieselfde straal om die omtrek af te merk
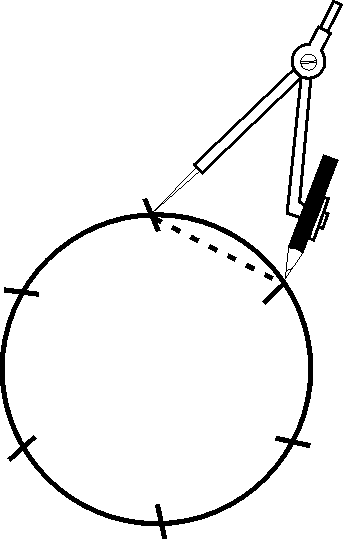
Verbind nou die punte (indien nodig)
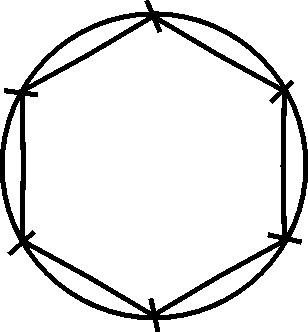
5.1
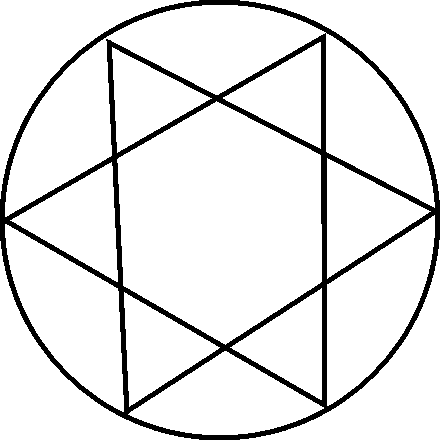
5.2
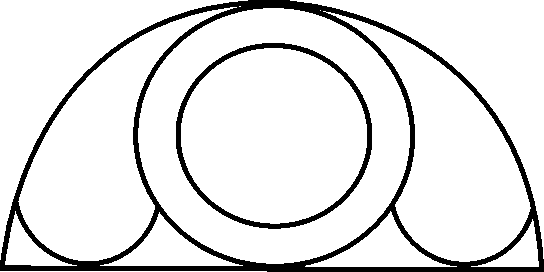
5.3
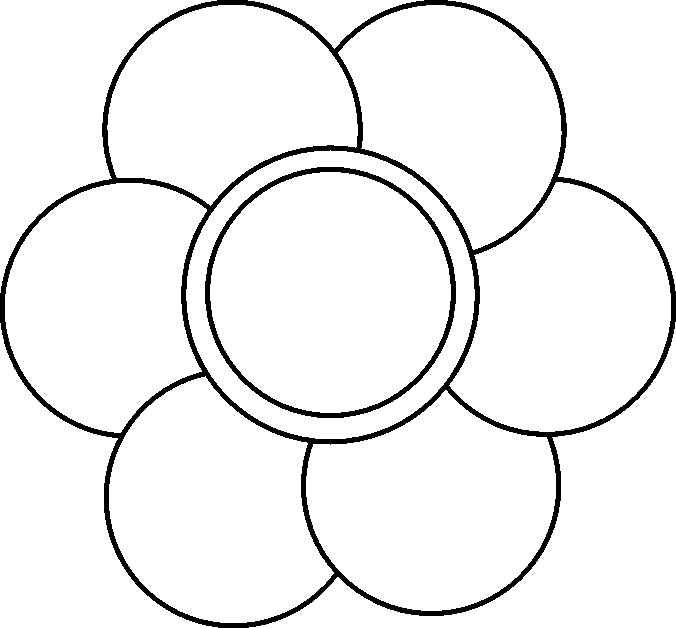
5.4
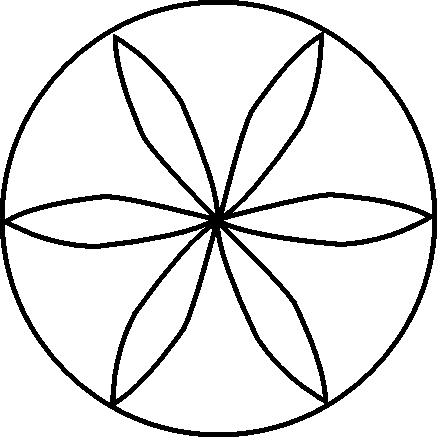
6. Ontwerp nou jou eie sirkel-patroon! Kleur dit netjies in:
Tyd vir selfassessering
Dit is belangrik dat ons sal weet of jy die werk wat ons tot dusver gedoen het, goed verstaan. Lees die onderstaande kriteria. Evalueer jouself op ‘n skaal van 1 – 4 deur ‘n sirkel om die toepaslike syfer te trek.
| Kriteria | 1 = Glad nie.2 = Net ‘n bietjie (min).3 = Goed.4 = Uitstekend. | ||||
| Ek kan die term “ewewydig” verduidelik. | 1 | 2 | 3 | 4 | |
| Ek kan die verskil tussen ‘n lyn en ‘n lynstuk verduidelik. | 1 | 2 | 3 | 4 | |
| Ek kan die volgende begrippe verduidelik: | |||||
| * skerphoek; | 1 | 2 | 3 | 4 | |
| * stomphoek; | 1 | 2 | 3 | 4 | |
| * regte hoek. | 1 | 2 | 3 | 4 | |
| Ek kan hoeke akkuraat: | |||||
| * met ‘n gradeboog meet; | 1 | 2 | 3 | 4 | |
| * met ‘n gradeboog trek. | 1 | 2 | 3 | 4 | |
| Ek kan die ooreenkomste tussen ‘n reghoek en ‘n parallelogram noem. | 1 | 2 | 3 | 4 | |
| Ek kan die verskille tussen ‘n reghoek en ‘n parallelogram noem. | 1 | 2 | 3 | 4 | |
| Ek kan die begrip “simmetries” verduidelik. | 1 | 2 | 3 | 4 | |
| Ek kan die term “rotasie-simmetrie” verduidelik. | 1 | 2 | 3 | 4 | |
| Ek kan die volgende begrippe verduidelik: | |||||
| * straal; | 1 | 2 | 3 | 4 | |
| * middellyn. | 1 | 2 | 3 | 4 | |
| Ek kon die figure vergroot en verklein. | 1 | 2 | 3 | 4 | |
| Ek kan patrone met sirkels teken. | 1 | 2 | 3 | 4 | |
Kom ons kyk na 3-Dimensionele figure.
Jy het seker al baie met ‘n dobbelsteen gespeel. Kyk of jy jou eie een kan maak. Trek die volgende ontvouing net so af. Knip dit uit en vou jou dobbel-steen. Skryf dan die nommers 1 – 6 op die kante. Onthou dat die nommerpare (1,6); (3,4) en (2,5) op die teenoorgestelde kante moet wees.
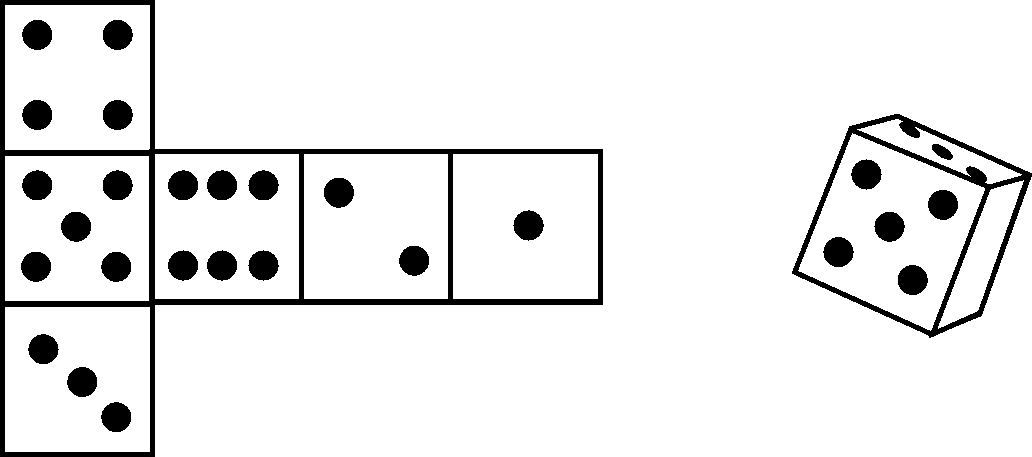
HET JY GEWEET?
Die dobbelsteen wat jy so pas gemaak het, is ‘n voorbeeld van ‘n kubus .
Kyk ook goed hierna:

Leeruitkomste 3: Die leerder is in staat om eienskappe van en verwantskappe tussen twee-dimensionele vorms en drie-dimensionele voorwerpe in ‘n verskeidenheid oriëntasies en posisies te beskryf en voor te stel.
Assesseringstandaard 3.3: Dit is duidelik wanneer die leerder twee-dimensionele vorms en drie-dimensionele voorwerpe wat in hierdie graad bestudeer word, ondersoek en vergelyk (individueel en/of as lid van ‘n groep), volgens die bostaande eienskappe deur die volgende te doen:
3.3.3: gebruik ‘n passer om sirkels, patrone in sirkels en patrone met sirkels te teken.

Notification Switch
Would you like to follow the 'Wiskunde graad 6' conversation and receive update notifications?