| << Chapter < Page | Chapter >> Page > |
Khởi đầu input xuất hiện trên băng thứ nhất, các băng khác chỉ toàn Blank.
Một máy Turing như vậy gọi là máy Turing với nhiều băng vô hạn hai chiều.
ĐỊNH LÝ 7.2 : Nếu L được nhận dạng bởi máy Turing nhiều băng vô hạn hai chiều thì nó cũng được nhận dạng bởi máy Turing một băng vô hạn hai chiều.
Chứng minh
Giả sử L được nhận diện bởi máy Turing k băng vô hạn hai chiều M1, ta xây dựng máy Turing M2 một băng với 2k rãnh, 2 rãnh sẽ mô phỏng một băng của M1 bằng cách: một rãnh giữ ký hiệu trên băng của M1 một rãnh kia giữ ký hiệu đánh dấu vị trí đầu đọc.
Mỗi phép chuyển của M1 được mô phỏng bằng M2 như sau:
M2 xuất phát tại vị trí trái nhất chứa ký hiệu đánh dấu đầu đọc, M2 quét sang phải, khi qua mỗi ô có đánh dấu vị trí đầu đọc nó ghi nhớ ký hiệu tại vị trí này và đếm số vị trí đầu đọc đã gặp. Khi M2 đi sang phải và đã đếm đủ k đầu đọc thì nó đã có đủ thông tin để xác định phép chuyển tương tự như M1, M2 lại quét từ phải sang trái, khi đi ngang qua mỗi ô có đánh dấu đầu đọc nó in ký hiệu thay thế ký hiệu tại đầu đọc (như M1) chuyển vị trí đánh dấu đầu đọc (như M1 chuyển đầu đọc của nó). Cuối cùng M2 đổi trạng thái trong bộ điều khiển của nó thành trạng thái mà M1 chuyển tới.
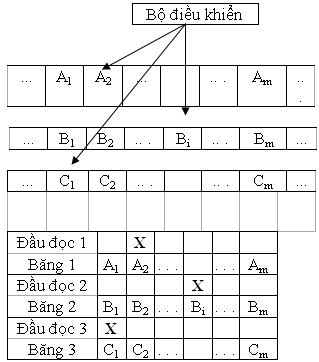
Hình 7.4 - Máy Turing 1 băng mô phỏng máy Turing 3 băng
Thí dụ 7..8 :Ngôn ngữ {ww w (0+1)*} có thể được chấp nhận bởi một máy Turing có 2 băng bằng cách như sau: Đầu tiên, nó chép lại chuỗi nhập ở băng thứ nhất lên băng thứ hai. Sau đó, trên băng thứ nhất đầu đọc chuyển dần từ cận trái sang cận phải của chuỗi, trong khi trên băng thứ hai đầu đọc lại chuyển ngược lại từ cận phải sang cận trái của chuỗi đó. Chuỗi được chấp nhận nếu suốt quá trình đó, các ký hiệu đọc được trên 2 băng luôn luôn đồng nhất.
Như ta đã biết, để đoán nhận ngôn ngữ này bằng TM một băng thì đầu đọc phải dịch chuyển tới lui rất nhiều lần để so sánh hai nửa của chuỗi nhập từ cả hai đầu băng. Như vậy, số bước dịch chuyển của nó xấp xỉ bằng bình phương độ dài chuỗi nhập, trong khi TM với 2 băng nhập chỉ cần thực hiện số bước chuyển tỷ lệ với độ dài của chuỗi nhập.
Máy Turing không đơn định có mô hình tương tự như mô hình gốc nhưng điểm khác biệt ở chỗ là trong mỗi lần chuyển, máy Turing có thể lựa chọn một trong một số hữu hạn các trạng thái kế tiếp, lựa chọn hướng chuyển đầu đọc, và lựa chọn ký hiệu in ra trên băng để thay thế ký hiệu vừa đọc được. Máy Turing trong mô hình gốc còn gọi là máy Turing đơn định.
ĐỊNH LÝ 7.3 : Nếu L được chấp nhận bởi máy Turing không đơn định M1 thì L cũng được chấp nhận bởi một máy Turing đơn định M2 nào đó.
Chứng minh
Với một trạng thái và một ký hiệu băng bất kỳ của M1, có một số hữu hạn các phép chuyển đến trạng thái kế tiếp, ta có thể đấnh số các trạng thái này là 1, 2, ... Gọi r là số lớn nhất của số các cách lựa chọn với một cặp trạng thái và ký kiệu bất kỳ. Ta có, mọi dãy các phép chuyển trạng thái đều được chỉ ra bằng một dãy chứa các số từ 1 đến r. Ngược lại một dãy hữu hạn bất kỳ gồm các số từ 1 đến r có thể biểu diễn cho một dãy các phép chuyển nào đó cũng có thể không. M2 được thiết kế có ba băng:

Notification Switch
Would you like to follow the 'Giáo trình tin học lý thuyết' conversation and receive update notifications?