| << Chapter < Page | Chapter >> Page > |
In the following exercises, compute each indefinite integral.
In the following exercises, find each indefinite integral by using appropriate substitutions.
In the following exercises, verify by differentiation that then use appropriate changes of variables to compute the integral.
Write an integral to express the area under the graph of from to e x and evaluate the integral.
Write an integral to express the area under the graph of between and and evaluate the integral.
In the following exercises, use appropriate substitutions to express the trigonometric integrals in terms of compositions with logarithms.
In the following exercises, evaluate the definite integral.
In the following exercises, integrate using the indicated substitution.
In the following exercises, does the right-endpoint approximation overestimate or underestimate the exact area? Calculate the right endpoint estimate R 50 and solve for the exact area.
[T] over
Exact solution: Since f is decreasing, the right endpoint estimate underestimates the area.
[T] over
Exact solution: Since f is increasing, the right endpoint estimate overestimates the area.
[T] over
Exact solution: Since f is increasing, the right endpoint estimate overestimates the area (the actual area is a larger negative number).
In the following exercises, for Find the area under the graph of between the given values a and b by integrating.
Find the area under the graph of the function between and
Compute the integral of and find the smallest value of N such that the area under the graph between and is, at most, 0.01.
The quantity is less than 0.01 when
Find the limit, as N tends to infinity, of the area under the graph of between and
Suppose that for all x and that f and g are differentiable. Use the identity and the chain rule to find the derivative of
Use the previous exercise to find the antiderivative of and evaluate
23
Show that if then the integral of from ac to bc is the same as the integral of from a to b .
The following exercises are intended to derive the fundamental properties of the natural log starting from the definition using properties of the definite integral and making no further assumptions.
Use the identity to derive the identity
We may assume that Then, Now make the substitution so and and change endpoints:
Use a change of variable in the integral to show that
Use the identity to show that is an increasing function of x on and use the previous exercises to show that the range of is Without any further assumptions, conclude that has an inverse function defined on
Pretend, for the moment, that we do not know that is the inverse function of but keep in mind that has an inverse function defined on Call it E . Use the identity to deduce that for any real numbers a , b .
Pretend, for the moment, that we do not know that is the inverse function of but keep in mind that has an inverse function defined on Call it E . Show that
Then, Since any number t can be written for some x , and for such t we have it follows that for any
The sine integral, defined as is an important quantity in engineering. Although it does not have a simple closed formula, it is possible to estimate its behavior for large x . Show that for
[T] The normal distribution in probability is given by where σ is the standard deviation and μ is the average. The standard normal distribution in probability, corresponds to Compute the left endpoint estimates of
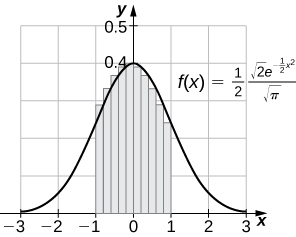
[T] Compute the right endpoint estimates of

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?