Discrete time aperiodic signals

Introduction

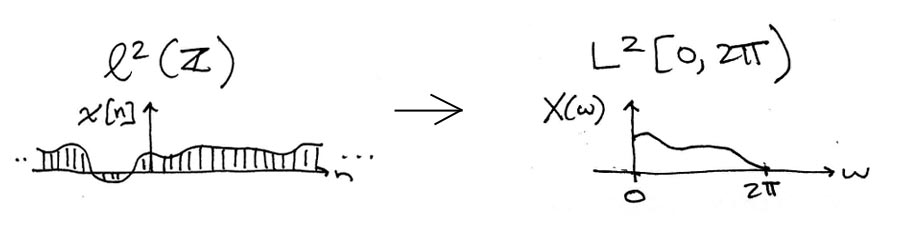
This module describes the type of signals acted on by the Discrete Time Fourier Transform.

Relevant spaces

The Discrete Time Fourier Transform maps arbitrary discrete time signals in $l^2(\mathbb{Z})$ to finite-length, discrete-frequency signals in $L^2(\left[0 , 2\pi \right))$ .

Periodic and aperiodic signals

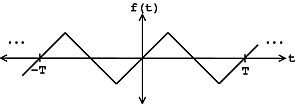
When a function repeats itself exactly after some given period, or cycle, we say it's periodic . A periodic function can be mathematically defined as:

Discrete-time periodic signal

We can think of periodic functions (with period $N$ ) two different ways:

1. as functions on all of $\mathbb{R}$

   

2. or, we can cut out all of the redundancy, and think of them as functions on an interval $\left[0 , N\right]()$ (or, more generally, $\left[a , a+N\right]()$ ). If we know the signal is N-periodic then all the information of the signal is captured by the above interval.

   

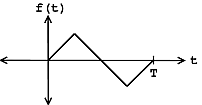
An aperiodic DT function, however, $f(n)$ does not repeat for any $N\in \mathbb{R}$ ; i.e. there exists no $N$ such that this equation holds. This broader class of signals can only be acted upon by the DTFT.

Suppose we have such an aperiodic function $f(n)$ . We can construct a periodic extension of $f(n)$ called $f_{\mathrm{No}}(n)$ , where $f(n)$ is repeated every $N_0$ seconds. If we take the limit as $N_0\to$∞ , we obtain a precise model of an aperiodic signal for which all rules that govern periodic signals can be applied, including Fourier Analysis (with an important modification). For more detail on this distinction, see the module on the Discete Time Fourier Transform .

Aperiodic signal demonstration

Conclusion

A discrete periodic signal is completely defined by its values in one period, such as the interval [0,N].Any aperiodic signal can be defined as an infinite sum of periodic functions, a useful definition that makes it possible to use Fourier Analysis on it by assuming all frequencies are present in the signal.