| << Chapter < Page | Chapter >> Page > |
Complex exponentials are some of the most important functions in our study of signals and systems. Their importance stems from their status as eigenfunctions of linear time invariant systems. Before proceeding, you should be familiar with complex numbers.
The complex exponential function will become a critical part of your study of signals and systems. Its general continuous form iswritten as
The mathematician Euler proved an important identity relating complex exponentials to trigonometric functions. Specifically, he discovered the eponymously named identity, Euler's formula, which states that
which can be proven as follows.
In order to prove Euler's formula, we start by evaluating the Taylor series for about , which converges for all complex , at . The result is
because the second expression contains the Taylor series for and about , which converge for all real . Thus, the desired result is proven.
Choosing this gives the result
which breaks a continuous time complex exponential into its real part and imaginary part. Using this formula, we can also derive the following relationships.
It has been shown how the complex exponential with purely imaginary frequency can be broken up into its real part and its imaginary part. Now consider a general complex frequency where is the attenuation factor and is the frequency. Also consider a phase difference . It follows that
Thus, the real and imaginary parts of appear below.
Using the real or imaginary parts of complex exponential to represent sinusoids with a phase delay multiplied by real exponential is often useful and is called attenuated phasor notation.
We can see that both the real part and the imaginary part have a sinusoid times a real exponential. We also know thatsinusoids oscillate between one and negative one. From this it becomes apparent that the real and imaginary parts of thecomplex exponential will each oscillate within an envelope defined by the real exponential part.
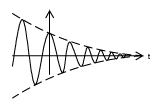
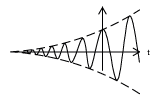
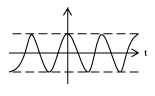
Continuous time complex exponentials are signals of great importance to the study of signals and systems. They can be related to sinusoids through Euler's formula, which identifies the real and imaginary parts of purely imaginary complex exponentials. Eulers formula reveals that, in general, the real and imaginary parts of complex exponentials are sinusoids multiplied by real exponentials. Thus, attenuated phasor notation is often useful in studying these signals.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?