| << Chapter < Page | Chapter >> Page > |
Werk in pare of groepe en ondersoek die geskiedenis van die ontwikkeling van meetkunde in die laaste 1500 jaar. Beskryf die verskeie stadiums van ontwikkeling enhoe verskeie kulture meetkunde gebruik het om hulle lewens te verbeter.
Die werke van die volgende mense moet ondersoek word:
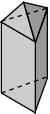
’n Piramide is ‘n geometriese soliede vorm met ‘n veelhoek as basis. Die basis is gekoppel aan die ‘n punt, wat die toppunt genoem word. Twee voorbeelde van piramides kan gesien word in die linkerhandse- en middelste figure in [link] . Die regterhandse figuur het ‘n toppunt wat gekoppel is aan ‘n sirkulêre (ronde) basis, en hierdie tipe meetkundige soliede vorm word ‘n konus genoem. Konusse is soortgelyk aan piramides behalwe dat hulle basisse rond is eerder as veelhoeke.

Oppervlakarea van ‘n Piramide
Khan akademie video van soliede geometriese volumes
Die oppervlakarea word bereken deur die area van elke vlak individueel bymekaar te tel.
Indien ‘n konus ‘n hoogte van het en ‘n basis radius van , wys dat die oppervlakareas is.
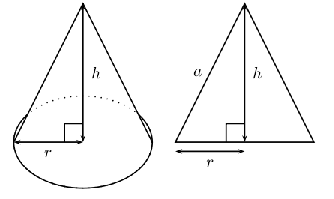
Die konus het twee vlakke: die basis en die kantvlakke. Die basis is ‘n sirkel met ‘n radius van en die kantvlakke kan oopgevlek word om ‘n sektor van ‘n sirkel te vorm.
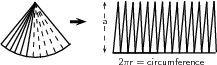
Die geboë oppervlak kan opgesny word in ‘n groot hoeveelheid dun driehoeke met hoogte ongeveer gelyk aan ( a word die skuinshoogte genoem). Die oppervlaktes van hierdie driehoeke te op tot basis hoogte(van ‘n klein driehoek) wat is
kan berekend word met die Stelling van Pythagoras. Daarom:
Volume of a Pyramid: Die volume van ‘n piramide kan bereken word deur :
waar die oppervlak van die basis is en die hoogte is.
’n Konus is soos ‘n piramide, en die volume van die konus word gegee deur:
’n Vierkantige piramide het volume
waar die kantlengte van die vierkantige basis.
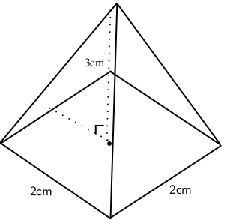
Wat is die volume van ‘n vierkantige piramide wat 3cm hoog is en ‘n kantlengte van 2cm het?
Die volume vir ‘n piramide is
waar die oppervlak van die basis is en die hoogte van die piramide is. Vir ‘n vierkantige basis beteken dit
waar die kantlengte van die vierkantige basis is.
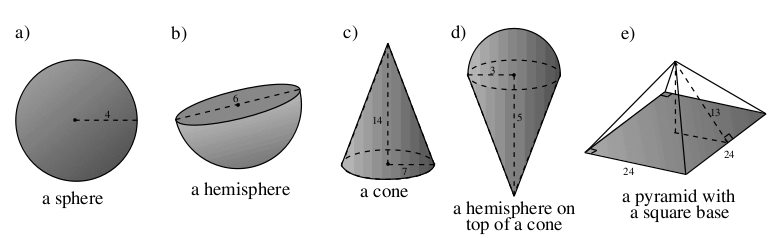
Ons aanvaar die volgende formules vir volume en oppervlak van ‘n sfeer (‘n sfeer is ‘n wiskundige term vir ‘n ronde bal).
Twee polinome is soortgelyk indien die volgende waar is:
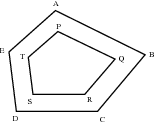
Poligone PQTU en PRSU is soortgelyk. Vind die waarde van
.
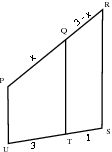
Aangesien die poligone soortgelyk is,

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 11)' conversation and receive update notifications?