| << Chapter < Page | Chapter >> Page > |
Analitiese meetkunde, ook bekend as koördinaatmeetkunde en vroëer bekend as Cartesiese meetkunde,is die studie van meetkunde op grond van die beginsels van algebra en die Cartesiese koördinaatstelsel. Dit is gemoeid metdie definisie van meetkundige figure op 'n numeriese wyse en onttrek numeriese inlligting uit die voorstelling. Sommige beskoudie ontwikkeling van analitiese meetkunde as die begin van moderne wiskunde.
As ons die koördinate van die hoekpunte van 'n figuur het, dan kan ons die figuur op die Cartesiese vlak teken. Byvoorbeeld, neem die vierhoek ABCD met koördinate A(1,1), B(1,3), C(3,3) en D(1,3) en stel dit voor op die Cartesiese vlak. Dit word getoon in [link] .
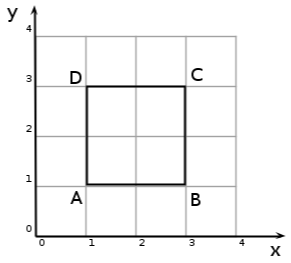
Om enige figuur voor te stel op die Cartesiese vlak, plaas ons 'n punt by elke gegewe koördinaat en verbind dan hierdie punte met reguitlyne. Een belangrike saak om op te let, is in die benoeming van die figuur. In bostaande voorbeeld, het ons die vierhoek ABCD genoem. Dit dui vir ons aan dat ons beweeg van punt A, na punt B, na punt C, na punt D en dan weer terug na punt A. Dus, wanneer jy gevra word om 'n figuur op die Cartesiese vlak te teken, moet jy hierdie benamingswyse gebruik. Soms word net sekere punte gegee en dan moet ons die ander punte vind deur gebruik te maak van die metodes wat ons verder in die hierdie hoofstuk gaan bespreek.
Een van die eenvoudigste dinge wat met analitiese meetkunde bereken kan word, is die afstand tussen twee punte. Afstand is a getal wat beskryf hoe ver twee punte van mekaar is. Byvoorbeeld, punt het as koördinate en punt het as koördinate. Hoe ver is die punte en van mekaar? In die figuur beteken dit, hoe lank is die stippellyn?
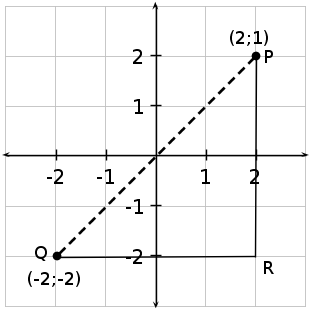
In die figuur kan gesien word dat lyn 3 eenhede lank is en lyn 4 eenhede. het 'n regte hoek . Dus kan die lengte van sy bereken word deur Stelling van Pythagoras te gebruik:
Die lengte van is gelyk aan die afstand tussen punte en .
As 'n veralgemening van die idee, neem aan dat enige punt is met as koördinate en is enige ander punt met as koördinate.
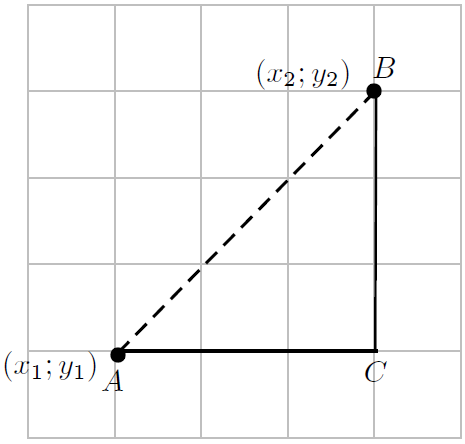
Die formule vir die berekening van die afstand tussen twee punte word as volg afgelei. Die afstand tussen twee punte en is die lengte van die lyn . Volgens die Stelling van Pythagoras, word die lengte van gegee deur:
Ons sien
Dan is
Gevolglik, vir enige twee punte, en , is die formule:
Afstand=
Deur die formule te gebruik, word die afstand tussen twee punte en met koördinate (2;1) en (-2;-2) as volg bereken. Gestel die koördinate van punt is en die koördinate van punt is . Dan is die afstand:

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?