| << Chapter < Page | Chapter >> Page > |
Find the volume of the solid bounded above by over the region enclosed by the curves and where is in the interval
cubic units
Finding the area of a rectangular region is easy, but finding the area of a nonrectangular region is not so easy. As we have seen, we can use double integrals to find a rectangular area. As a matter of fact, this comes in very handy for finding the area of a general nonrectangular region, as stated in the next definition.
The area of a plane-bounded region is defined as the double integral
We have already seen how to find areas in terms of single integration. Here we are seeing another way of finding areas by using double integrals, which can be very useful, as we will see in the later sections of this chapter.
Find the area of the region bounded below by the curve and above by the line in the first quadrant ( [link] ).
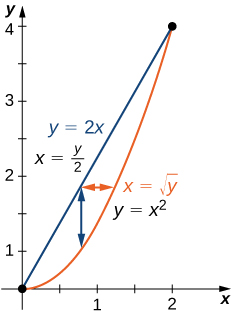
We just have to integrate the constant function over the region. Thus, the area of the bounded region is or
Find the area of a region bounded above by the curve and below by over the interval
square units
We can also use a double integral to find the average value of a function over a general region. The definition is a direct extension of the earlier formula.
If is integrable over a plane-bounded region with positive area then the average value of the function is
Note that the area is
Find the average value of the function on the region bounded by the line and the curve ( [link] ).
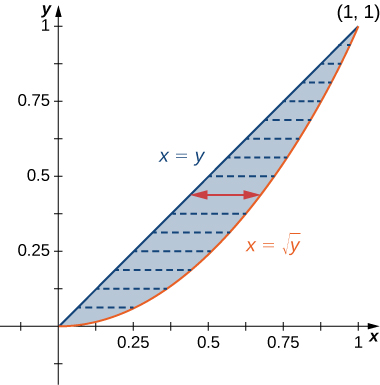
First find the area where the region is given by the figure. We have
Then the average value of the given function over this region is
Find the average value of the function over the triangle with vertices
An improper double integral is an integral where either is an unbounded region or is an unbounded function. For example, is an unbounded region, and the function over the ellipse is an unbounded function. Hence, both of the following integrals are improper integrals:
In this section we would like to deal with improper integrals of functions over rectangles or simple regions such that has only finitely many discontinuities. Not all such improper integrals can be evaluated; however, a form of Fubini’s theorem does apply for some types of improper integrals.
If is a bounded rectangle or simple region in the plane defined by and also by and is a nonnegative function on with finitely many discontinuities in the interior of then

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?