| << Chapter < Page | Chapter >> Page > |
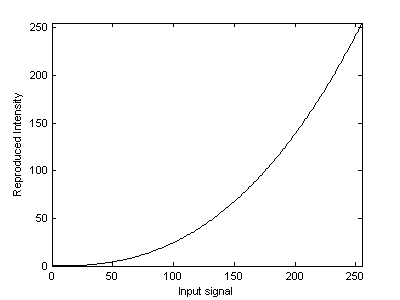
In order to achieve the correct reproduction of intensity, this nonlinearity must be compensated by a process known as correction . Images that are not properly corrected usually appear too light or too dark.If the value of is available, then the correction process consists of applying the inverse of [link] . This is a straightforward pixel transformation,as we discussed in the section "Pointwise Transformations" .
Write a Matlab function that will correct an image by applying the inverse of [link] . The syntax should be
B = gammCorr(A,gamma)
where is the uncorrected image, is the of the device, and is the corrected image. (See the hints in "Pointwise Transformations" .)
The file dark.tif is an image that has not been corrected for your monitor. Download this image, and read it into Matlab.Display it and observe the quality of the image.
Assume that the
for your monitor is 2.2.
Use your
gammCorr function to
correct the image for your monitor, and display theresultant image. Did it improve the quality of the picture?
gammCorr .Sometimes, we need to process images to improve their appearance. In this section, we will discuss two fundamental image enhancementtechniques: image smoothing and sharpening .
Smoothing operations are used primarily for diminishing spurious effects that may be presentin a digital image, possibly as a result of a poor sampling system or a noisy transmission channel. Lowpass filtering is a populartechnique of image smoothing.
Some filters can be represented as a 2-D convolution of an image with the filter's impulse response .
Some typical lowpass filter impulse responses are shown in [link] , where the center element corresponds to . Notice that the terms of each filter sum to one.This prevents amplification of the DC component of the original image.The frequency response of each of these filters is shown in [link] .
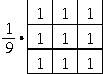
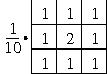
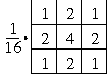
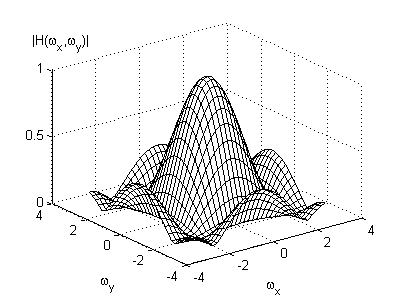
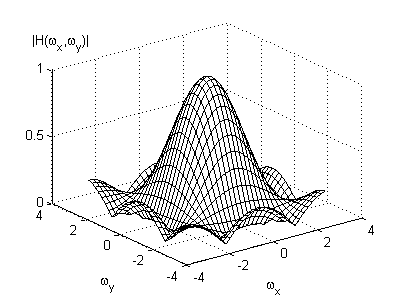
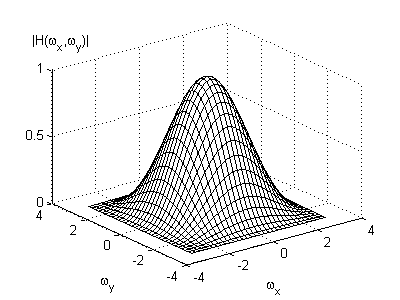
An example of image smoothing is shown in [link] , where the degraded image is processed by the filter shown in [link] . It can be seen thatlowpass filtering clearly reduces the additive noise, but at the same time it blurs the image. Hence, blurring is a major limitation of lowpass filtering.



In addition to the above linear filtering techniques, images can be smoothed by nonlinear filtering, such as mathematical morphological processing. Median filtering is one of the simplest morphological techniques, and is useful in the reduction of impulsive noise.The main advantage of this type of filter is that it can reduce noise while preserving the detail of the original image.In a median filter, each input pixel is replaced by the median of the pixels contained in a surrounding window. This can be expressed by

Notification Switch
Would you like to follow the 'Purdue digital signal processing labs (ece 438)' conversation and receive update notifications?