| << Chapter < Page | Chapter >> Page > |
In this section we will discuss techniques using spreadsheet for conducting an hypothesis test for one sample mean, population standard deviation known; a one sample mean, population standard deviation unknown: and for a one sample proportion,
You can set up a worksheet in Excel to compute the one sample tests by using one of the following formulas in Excel or Google Spreadsheet
| Function | Excel Formula | Google Spreadsheet formula |
|---|---|---|
| z-test: for one sample mean population standard deviation known | =z.test(array,x,sigma) where array is the sample data identifying the first cell address and the last cell address in the data set, x is the value you want to test, and sigma is populations known standard deviation. | =ztest(array,x,sigma) where array is the sample data identifying the first cell address and the last cell address in the data set, x is the value you want to test, and sigma is populations known standard deviation. |
| t-test: for a one sample mean population standard deviation unknown. | =confidence.t(alpha, standard deviation, number in sample) | No built in formula |
| z-test: one sample proportion | There is no built in formula. . . we will calculate using model below = p-hat±(critical value z-score*sqrt((p-hat*(1-p-hat)/n) | There is no built in formula. . . we will calculate using model below = p-hat±(critical value z-score*sqrt((p-hat*(1-p-hat)/n) |
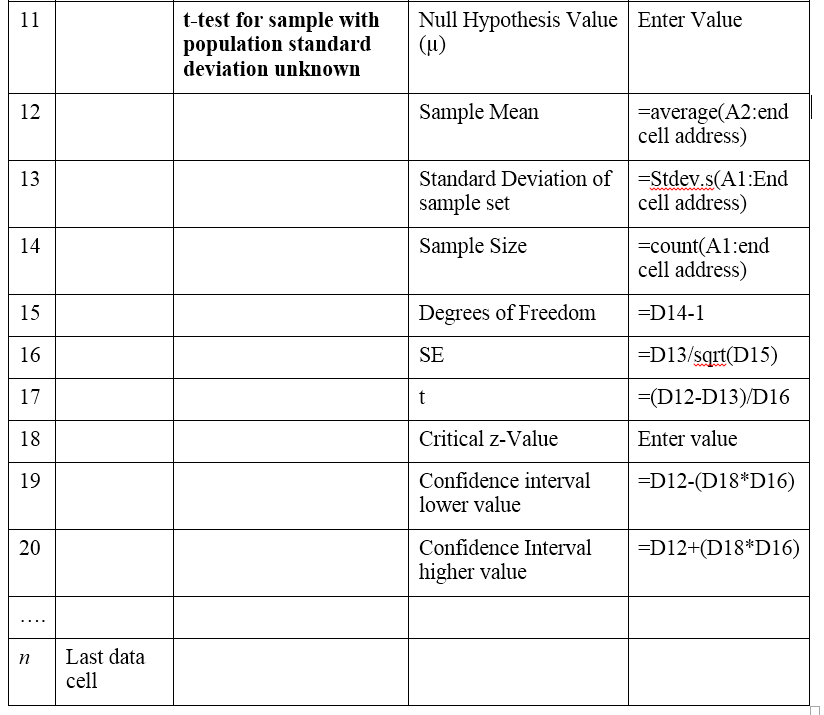
In an Excel or Google Spreadsheet you would arrange your data as demonstrated in the following columns. The following is labeled as though it was an Excel or Google Spreadsheet.
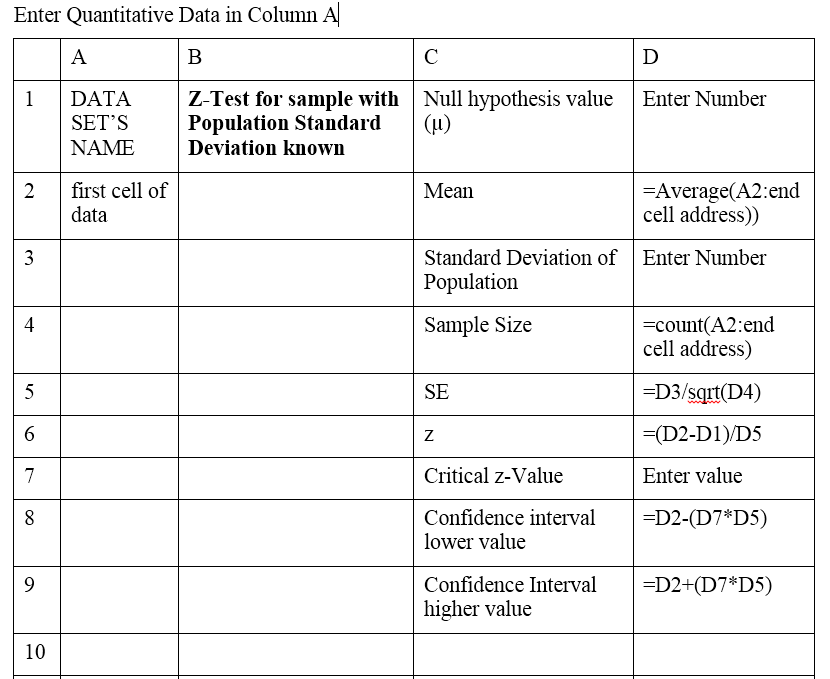
Quantitative Data in Column A

To graph T-test and Z-test use the “Statistics Online Computational Resources (SOCR)”(just as in the previous chapter)at
http://socr.ucla.edu/htmls/SOCR_Distributions.html has in the dropdown menu for SOCR distribution the normal distribution and for a Student’s t-distribution. For a normal distribution, you will need to have your mean and standard deviation and again your right and left cut off values (which in this case will be your critical values). For a Student’s t-distribution, you will need to have degrees of freedom and again your right and left cut off values (which in this case will be your critical values). Below is a graph of the Student’s t-distribution. We have used the example from 8.6 Two column Model step by step example for this demonstration. The degrees of freedom were 14 and a 95% confidence interval. We used the t-table to determine the left and right cut off values. In this instance two tailed confidence interval of 95% with 14 degrees for freedom is minus and plus 2.145.

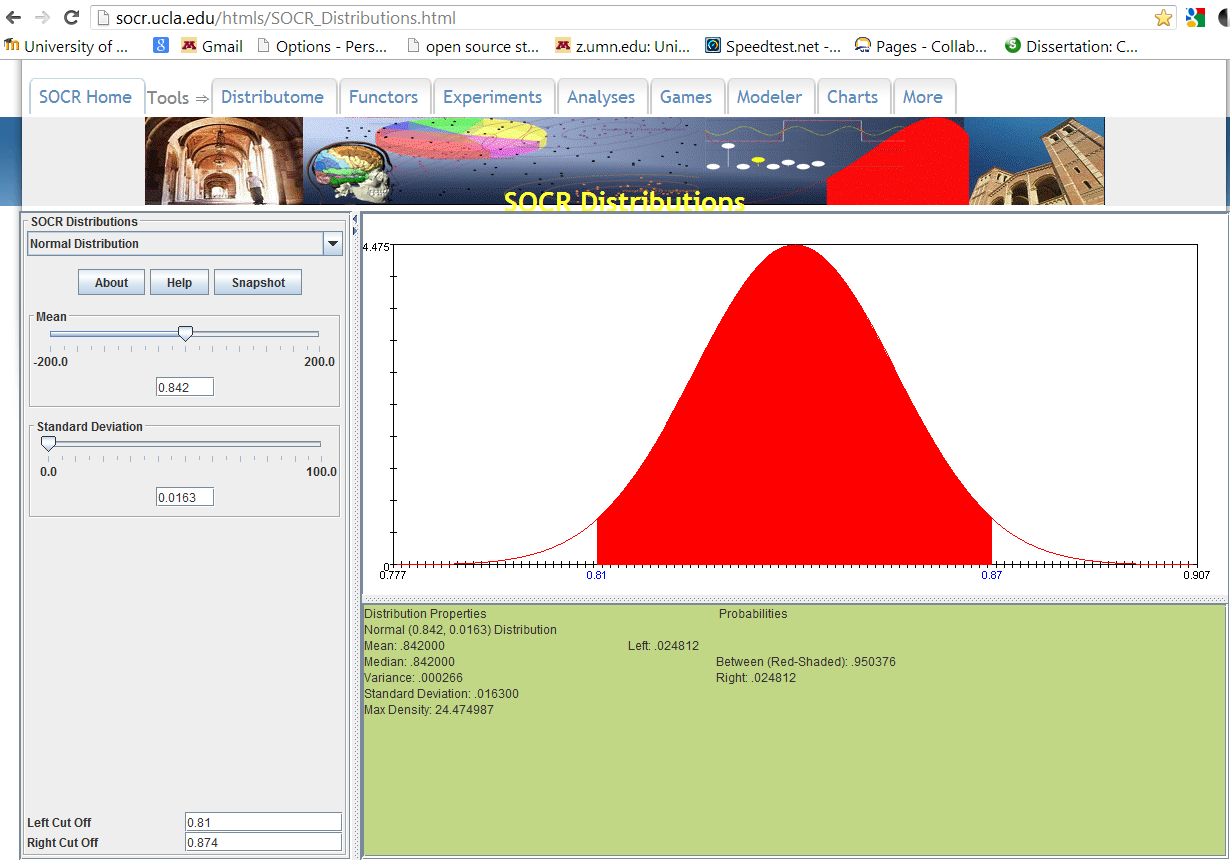
This next example is using the normal distribution for determining the confidence interval for a population proportion. The normal density curve here has the population proportion as the mean (p or p-hat) and the standard deviation (the square root of (p(1-p)/n). We have demonstrated the example 8.8 to show you how this looks in SOCR. For this problem the mean proportion was .842 and the critical z-value for a 95% confidence interval was ± 0.032 or (0.81, 0.874).
At your computer, try to use some of these tools to work out your homework problems or check homework that you have completed to see if the results are the same or similar.

Notification Switch
Would you like to follow the 'Collaborative statistics using spreadsheets' conversation and receive update notifications?