| << Chapter < Page | Chapter >> Page > |
Fourier series is a useful orthonormal representation on especiallly for inputs into LTI systems. However, it is ill suited for some applications, i.e. image processing (recall Gibb's phenomena ).
Wavelets , discovered in the last 15 years, are another kind of basis for and have many nice properties.
Fourier series - give frequency information. Basis functions last the entire interval.
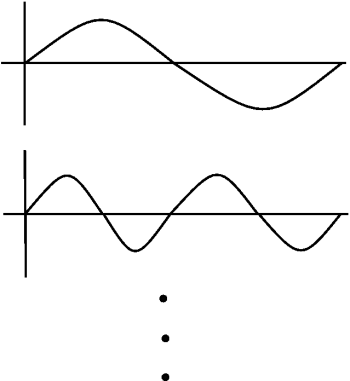
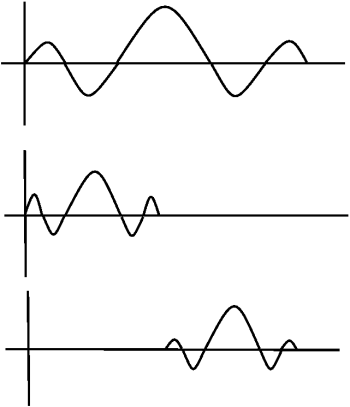
Wavelets - basis functions give frequency info but are local in time.
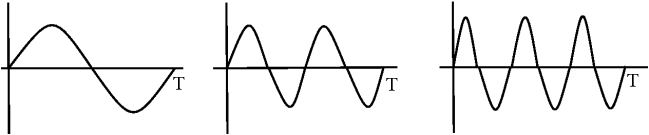
In Fourier basis, the basis functions are harmonic multiples of
In Haar wavelet basis , the basis functions are scaled and translated versions of a "mother wavelet" .
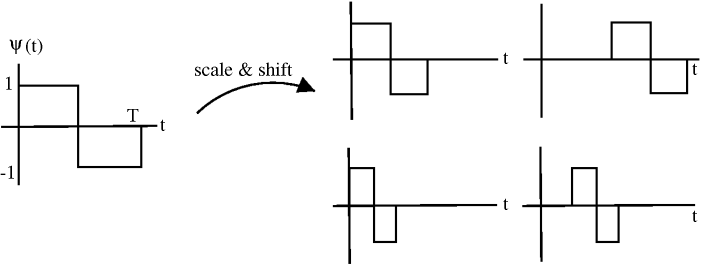
Basis functions are indexed by a scale j and a shift k.
Let Then
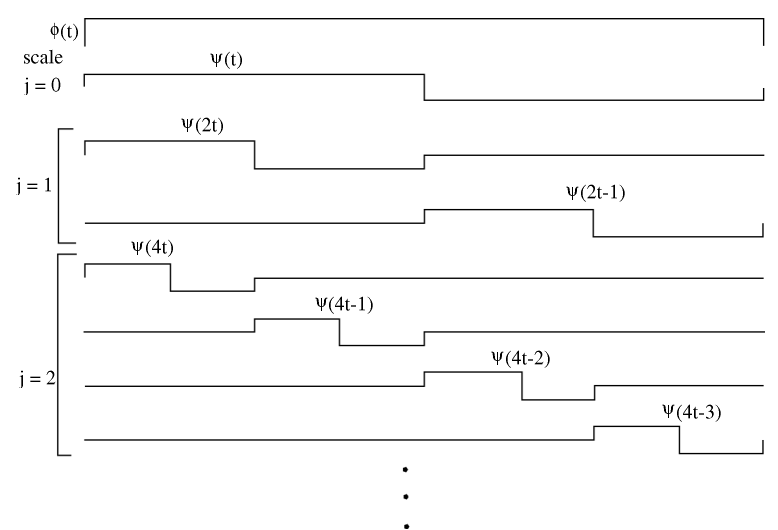
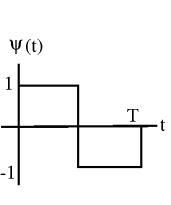
Let
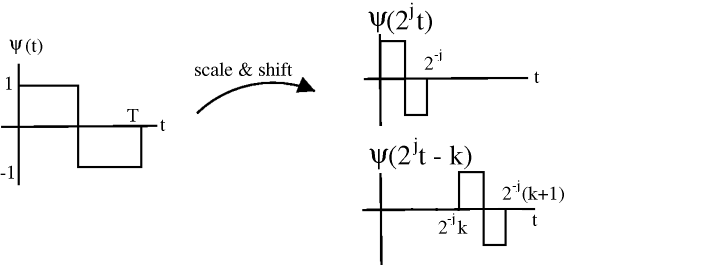
Larger → "skinnier" basis function, , shifts at each scale:
Check: each has unit energy
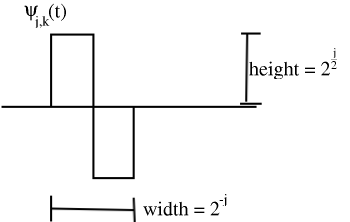
Any two basis functions are orthogonal.
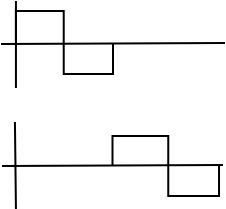
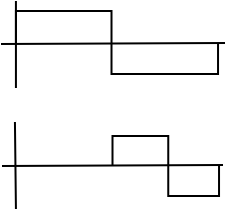
Also, span
Using what we know about Hilbert spaces : For any , we can write

Notification Switch
Would you like to follow the 'Intro to digital signal processing' conversation and receive update notifications?