| << Chapter < Page | Chapter >> Page > |
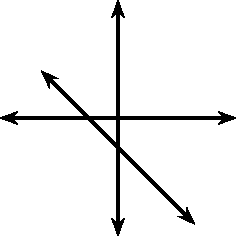
Funksies met die algemene vorm word reguitlyn funksies genoem. In die vergelyking, , is en konstantes en het verskillende invloede op die grafiek van die funksie. Die algemene grafiek van so 'n funksie word gegee in [link] vir die funksie .
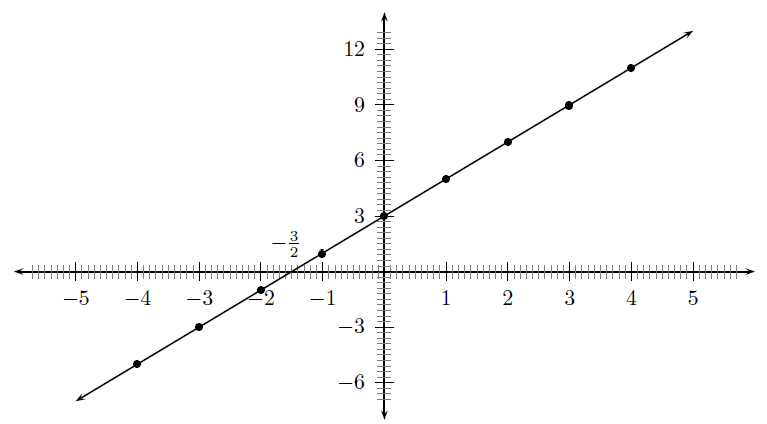
Jy behoort te vind dat die waarde van die helling van die grafiek beïnvloed. Soos vermeerder, vermeerder die helling van die grafiek ook. Indien sal die grafiek vermeerder van links na regs (opwaartse helling). Indien sal die grafiek verminder van links na regs (afwaartse helling). Dit is hoekom daar na verwys word as die helling of die gradiënt van 'n reguitlynfunksie.
Jy behoort ook te vind dat die waarde van die punt bepaal waar die grafiek die -as sny. Om hierdie rede, staan bekend as die y-afsnit .
Die verskillende eienskappe word opgesom in [link] .
 |
 | |
 |
 |
Vir , is die definisieversameling , omdat daar geen waarde is van waarvoor ongedefinieërd is nie.
Die waardeversameling van is ook omdat daar geen waarde van waarvoor ongedefinieërd is nie.
Byvoorbeeld, die definisieversameling van is omdat daar geen waardes is van waarvoor ongedefinieërd is nie. Die waardeversameling van is .
Vir funksies van die vorm, word die metode om die afsnitte met die - en -asse te bereken, uiteengesit.
Die -afsnitte word as volg bereken:
Byvoorbeeld, die -afsnit van word bepaal deur te stel en dan op te los:
Die -afsnit word as volg bereken:
Byvoorbeeld, die -afsnit van word gegee deur in te stel en dan op te los:
Die grafiek van 'n reguitlynfunksie het nie draaipunte nie.
Die grafieke van reguitlynfunksies het gewoonlik nie simmerie-asse nie.
Om die grafieke van die vorm te skets, moet ons die volgende drie eienskappe vind:
Slegs twee punte word benodig om 'n reguitlyn te trek. Die maklikste punte is die -afsnit (waar die lyn die -as sny) en die -afsnit.
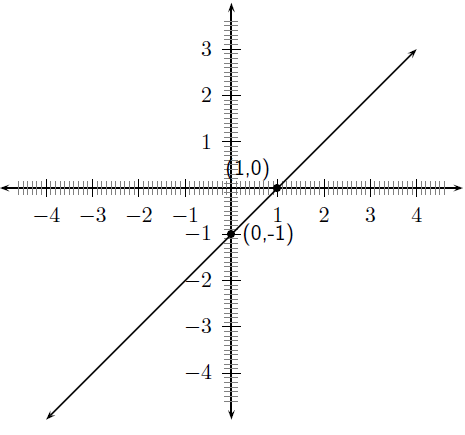
Byvoorbeeld, skets die grafiek van . Merk duidelik die afsnitte.
Eerstens bereken ons dat . Dit beteken die grafiek gaan 'n opwaartse helling hê.
Die -afsnit word bepaal deur te stel en is vroeër bereken as . Die -afsnit word bepaal deur te stel en is vroeër bereken as .
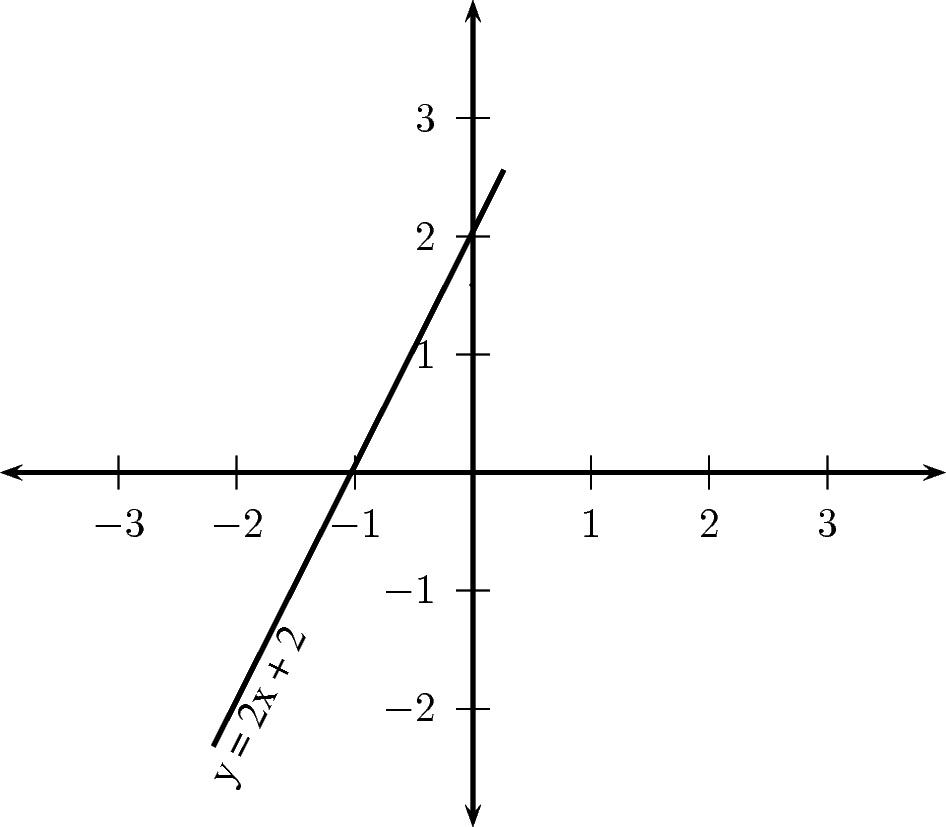
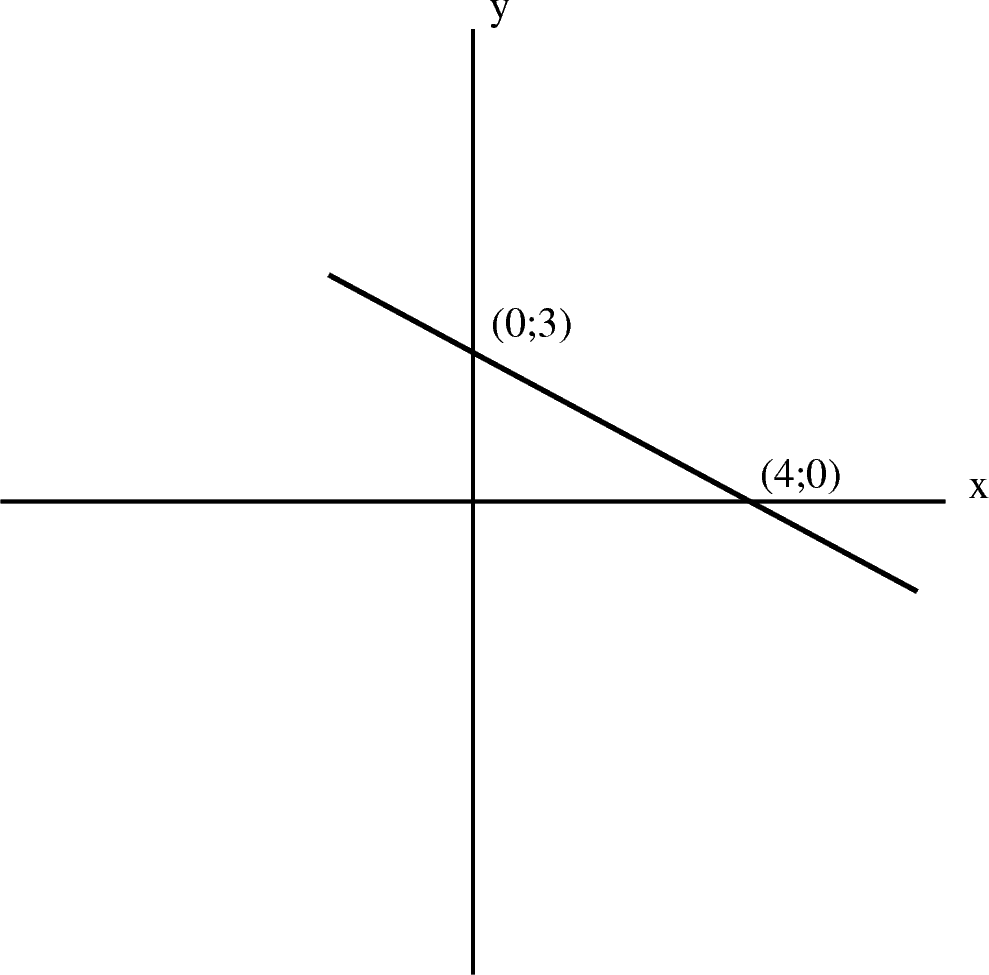
Teken die grafiek van .
Om die y-afsnit te vind, stel .
Om die x-afsnit te kry, stel .

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?