| << Chapter < Page | Chapter >> Page > |
Suppose you are trying to find out what percentage of South Africa's population owns a car. One way of doing this might be to send questionnaires to peoples homes, asking them whether they own a car. However, you quickly run into a problem: you cannot hope to send every person in the country a questionnaire, it would be far to expensive. Also, not everyone would reply. The best you can do is send it to a few people, see what percentage of these own a car, and then use this to estimate what percentage of the entire country own cars. This smaller group of people is called the sample population .
The sample population must be carefully chosen, in order to avoid biased results. How do we do this?
First, it must be representative . If all of our sample population comes from a very rich area, then almost all will have cars. But we obviously cannot conclude from this that almost everyone in the country has a car! We need to send the questionnaire to rich as well as poor people.
Secondly, the size of the sample population must be large enough. It is no good having a sample population consisting of only two people, for example. Both may very well not have cars. But we obviously cannot conclude that no one in the country has a car! The larger the sample population size, the more likely it is that the statistics of our sample population corresponds to the statistics of the entire population.
So how does one ensure that ones sample is representative? There are a variety of methods available, which we will look at now.
In Grade 11 we recorded two sets of data (bivariate data) on a scatter plot and then we drew a line of best fit as close to as many of the data items as possible. Regression analysis is a method of finding out exactly which function best fits a given set of data. We can find out the equation of the regression line by drawing and estimating, or by using an algebraic method called “the least squares method”, available on most scientific calculators. The linear regression equation is written (we say y-hat) or . Of course these are both variations of a more familiar equation .
Suppose you are doing an experiment with washing dishes. You count how many dishes you begin with, and then find out how long it takes to finish washing them. So you plot the data on a graph of time taken versus number of dishes. This is plotted below.
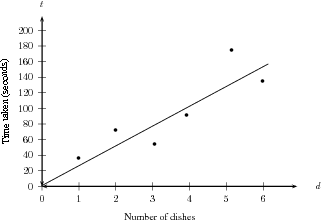
If is the time taken, and the number of dishes, then it looks as though is proportional to , ie. , where is the constant of proportionality. There are two questions that interest us now.
In this chapter, we answer both of these questions, using the techniques of regression analysis .
Phet simulation for curve fitting
Use the data given to draw a scatter plot and line of best fit. Now write down the equation of the line that best seems to fit the data.
| x | 1,0 | 2,4 | 3,1 | 4,9 | 5,6 | 6,2 |
| y | 2,5 | 2,8 | 3,0 | 4,8 | 5,1 | 5,3 |
The first step is to draw the graph. This is shown below.
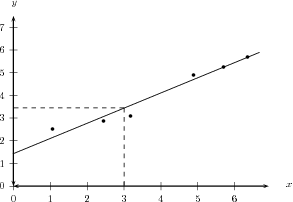
The equation of the line is
From the graph we have drawn, we estimate the y-intercept to be 1,5. We estimate that when . So we have that points and lie on the line. The gradient of the line, , is given by
So we finally have that the equation of the line of best fit is

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 maths' conversation and receive update notifications?