| << Chapter < Page | Chapter >> Page > |
We can make use of conversion skills with denominate numbers to make measurements of geometric figures such as rectangles, triangles, and circles. To make these measurements we need to be familiar with several definitions.



To find the perimeter of a polygon, we simply add up the lengths of all the sides.
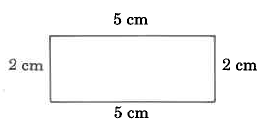
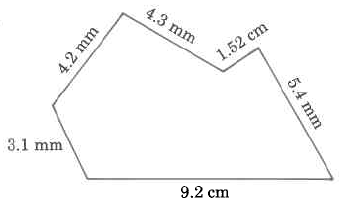
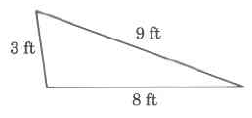
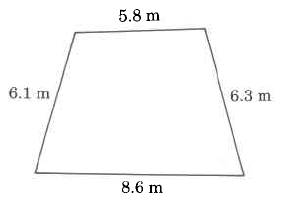
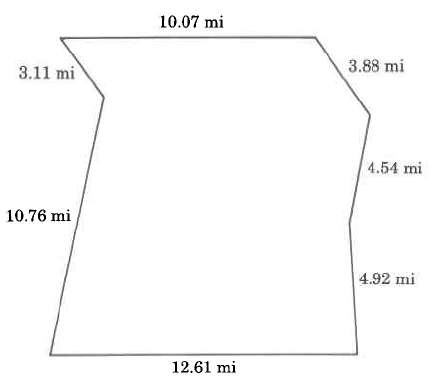
Find the perimeter of each polygon.
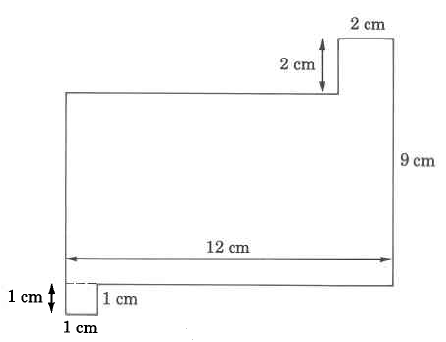
Our first observation is that three of the dimensions are missing. However, we can determine the missing measurements using the following process. Let A, B, and C represent the missing measurements. Visualize
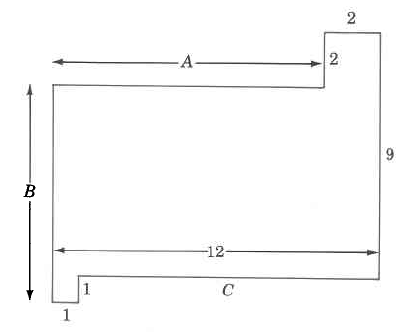
Find the perimeter of each polygon.
20 ft
26.8 m
49.89 mi
The symbol , read "pi," represents the nonterminating, nonrepeating decimal number 3.14159 … . This number has been computed to millions of decimal places without the appearance of a repeating block of digits.
For computational purposes, is often approximated as 3.14. We will write to denote that is approximately equal to 3.14. The symbol "≈" means "approximately equal to."
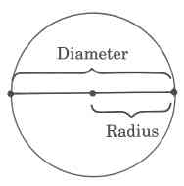
To find the circumference of a circle, we need only know its diameter or radius. We then use a formula for computing the circumference of the circle.
Formulas are usually composed of letters that represent important, but possibly unknown, quantities.
If , , and represent, respectively, the circumference, diameter, and radius of a circle, then the following two formulas give us directions for computing the circumference of the circle.
Find the exact circumference of the circle.
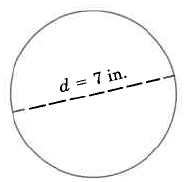
Use the formula .
By commutativity of multiplication,
, exactly
This result is exact since has not been approximated.
Find the approximate circumference of the circle.
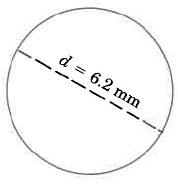
Use the formula .
This result is approximate since has been approximated by 3.14.
Find the approximate circumference of a circle with radius 18 inches.
Since we're given that the radius, , is 18 in., we'll use the formula .
Find the approximate perimeter of the figure.
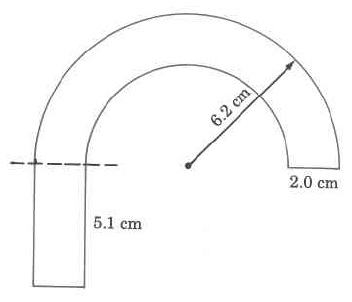
We notice that we have two semicircles (half circles).
The larger radius is 6.2 cm.
The smaller radius is .
The width of the bottom part of the rectangle is 2.0 cm.
Find the exact circumference of the circle.
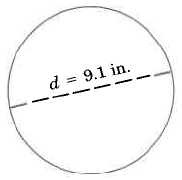
9.1 in.
Find the approximate circumference of the circle.
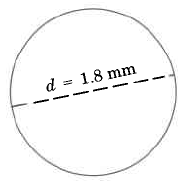
5.652 mm
Find the approximate circumference of the circle with radius 20.1 m.
126.228 m
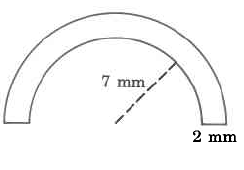
Find the approximate outside perimeter of
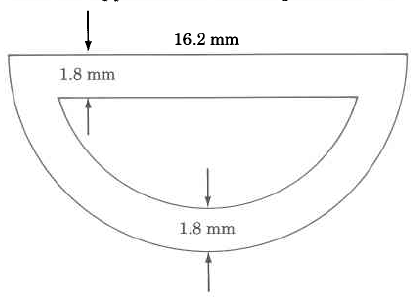
41.634 mm
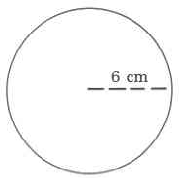
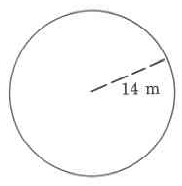
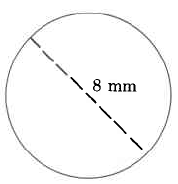
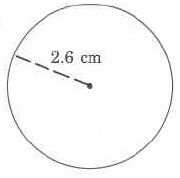
Find each perimeter or approximate circumference. Use .
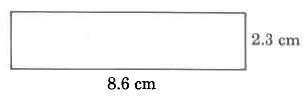
21.8 cm
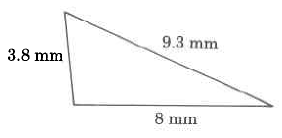
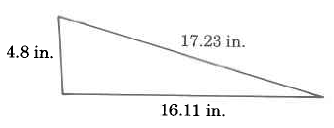
38.14 inches
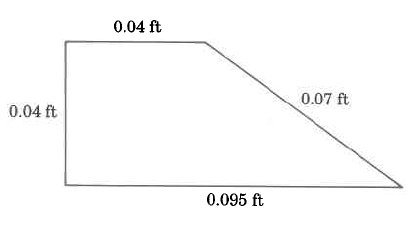
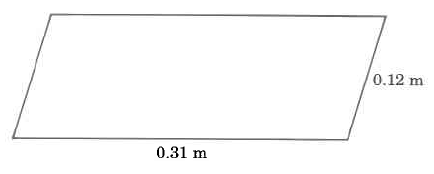
0.86 m
87.92 m
16.328 cm
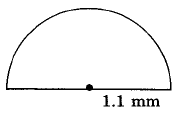
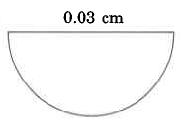
0.0771 cm
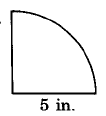
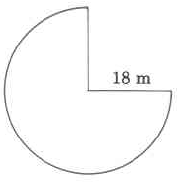
120.78 m
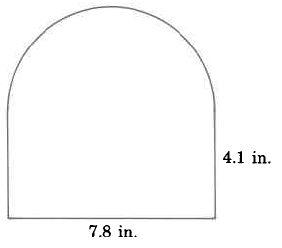
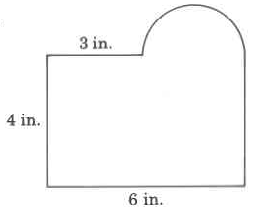
21.71 inches
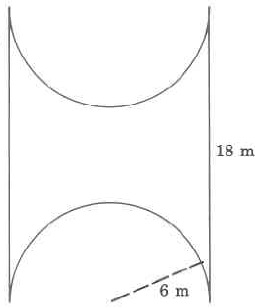
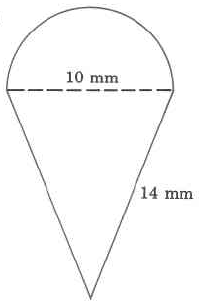
43.7 mm
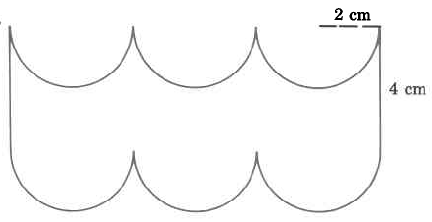
45.68 cm
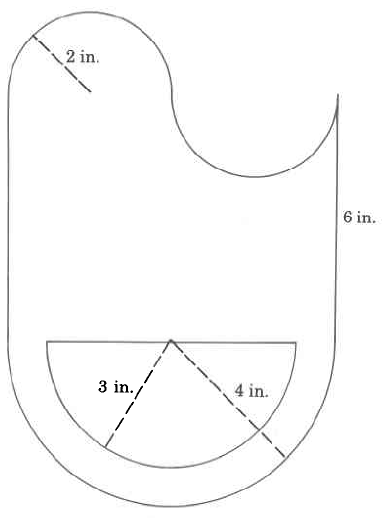
( [link] ) Find the value of .
8.5 or or
( [link] ) Find the value of .
( [link] ) Convert to a decimal.
0.875
( [link] ) What is the name given to a quantity that is used as a comparison to determine the measure of another quantity?
( [link] ) Add 42 min 26 sec to 53 min 40 sec and simplify the result.
1 hour 36 minutes 6 seconds

Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?