Whole numbers: place value and writing numbers

Numbers and numerals

Numbers that are formed using only the following digits are called whole numbers :

0 1 2 3 4 5 6 7 8 9

The whole numbers in order are:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

The three dots at the end mean “and so on in the same pattern.”

The whole numbers can be visualized by constructing a number line. To construct a number line, we simply draw a straight line and choose any point on the line and label it 0. This point is called the origin. We then choose some convenient length, and moving to the right, mark off consecutive and equal intervals (parts) along the line starting at 0. We label each new interval endpoint with the next whole number.

We can visually display a whole number by drawing a closed circle at the point labeled with that whole number. Another phrase for visually displaying a whole number is graphing the whole number. The word graph means to “visually display.”

The names for whole numbers

The Hindu-Arabic numerals 0 1 2 3 4 5 6 7 8 9 are called digits. We can form any number in the number system by selecting one or more digits and placing them in certain positions. Each position has a particular value. The Hindu mathematician who devised the system in about 500 A.D. stated that “from place to place each is ten times the preceding.” It is for this reason that our number system is called a positional number system with base ten.

When numbers are composed of more than three digits, commas are sometimes used to separate the digits into groups of three (such as 1,465,345). These groups of three are called periods, and they greatly simplify reading numbers.

In the Hindu-Arabic numeration system, a period has a value assigned to each of its three positions, and the values are the same for each period. The position values are from right to left ones, tens, hundreds.

Each period contains a position for the values of one, ten, and hundred. Notice that, in looking from right to left, the value of each position is ten times the preceding. Each period has a particular name.

As we continue from right to left, there are more periods. The five periods listed above are the most common, and in our study of introductory mathematics, they are sufficient.

The following diagram illustrates our positional number system to trillions. (There are, to be sure, other periods.)

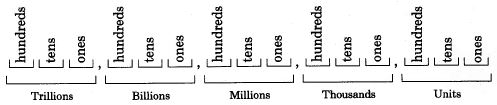
In our positional number system, the value of a digit is determined by its position in the number.

Because our number system is a positional number system, reading and writing whole numbers is quite simple.

Reading whole numbers

To convert a number that is formed by digits into a verbal phrase, use the following method:

1. Beginning at the right and working right to left, separate the number into distinct periods by inserting commas every three digits (e.g. “123456” becomes “123,456”).
2. Beginning at the left, read each period individually, saying the period name.

Here are a few examples for writing the numbers as words.

Example 1

Write out 42958.

1. Beginning at the right, we can separate this number into distinct periods by inserting a comma between the 2 and 9, which is 42,958.
2. Beginning at the left, we read each period individually:
   • Thousands period: __ 4 2 → Forty-two thousand,
   • Units period: 9 5 8 → nine hundred fifty-eight.

Solution: Forty-two thousand, nine hundred fifty-eight.

Example 2

Write out 307991343.

1. Beginning at the right, separate this number into distinct periods by placing commas between the 1 and 3, and the 7 and 9, resulting in “307,991,343”.
2. Beginning at the left, read each period individually.

• Millions period: 3 0 7 → Three hundred seven million,
• Thousands period: 9 9 1 → nine hundred ninety-one thousand,
• Units period: 3 4 3 → three hundred forty-three.

Solution: Three hundred seven million, nine hundred ninety-one thousand, three hundred forty-three

Example 3

Write out 36000000001.

1. Beginning at the right, separate this number into distinct periods by placing commas, resulting in 36,000,000,001.
2. Beginning at the left, read each period individually.

• Trillions period: __ 3 6 → Thirty-six trillion,
• Billions period: 0 0 0 → zero billion,
• Millions period: 0 0 0 → zero million,
• Thousands period: 0 0 0 → zero thousand,
• Units period: 0 0 1 → one.

Solution: Thirty-six trillion, one.

Exercises

Write out each number in words.

For the following exercises, write the numbers for the following text.